[ Привет, физматика! ] [ Что нового на сайте ] [ Разобраться в теории ] [ Если не решается задача ] [ Тесты на понятливость ] [ Ну очень трудные задачи ] [ Короткие заметки ] [ Статьи ] [ Форумы ] [ О нас пишут ]

Беседы о 4-х мерной геометрии

Аннотация

Но как проделать то же для других фигур?

Часть 1

Куб и простейшие фигуры

* Модель 4х-мерного куба (гиперкуба)

** Первые соображения

Читая в школьную пору книжки по занимательной математике и удивляясь рассказам М.Гарднера о приключениях во Флатландии – мире, где нет 3-его измерения и поэтому, встретившись с человеком, нельзя с ним разойтись, можно только перелезть, я задавался вопросом: а нельзя хоть краешком глаза заглянуть в мир 4-мерный? Ну например, увидеть, как выглядит 4х-мерный куб? Относительно куба задача казалась простой, потому что он должен быть как две капли воды похож на куб 3х-мерный с тем лишь отличием, что все 2х-мерные элементы 2-го превращались в 3х-мерные. И это тем более так, поскольку 2х-мерные элементы 3х-мерного куба (далее будем называть его просто куб, 4х-мерный куб – гиперкуб), его грани, представляют из себя квадрат, который есть ни что иное, как 2х-мерный аналог куба.

*** Развертка

Совершенно очевидно, что развертка гиперкуба представляет из себя 6 кубов, соединенных крестом, так же как и развертка куба представляет из себя аналогичную конструкцию их квадратов. Но здесь стоит оговориться – это будет, с позволения сказать, объемная развертка, а не плоская.

Потому что плоских (наружных) граней у гиперкуба должно быть 8, по 2 на каждое измерения. Стоп, но тогда у гиперкуба есть еще какие-то внутренние плоские грани?

*** Изображение и модель

Так вот, в 3х-мерном мире эту объемную развертку свернуть в гиперкуб не удается – мешает отсутствие 4-го измерения. Однако в 3х-мерном мире мы можем полюбоваться на 3-мерную модель гиперкуба, так же как любуемся 2х-мерными изображениями куба. Мы, конечно, можем плоско изобразить и 3х-мерную модель гиперкуба, но это изображение будет нести меньше информации о гиперкубе.

Новая тема: если изображение бывает не только 2х-мерным, но и 3х-мерным (и тогда мы называем его моделью), то не является ли видимый нами мир всего лишь изображением некоего гипермира?

И чем тогда мир отличается от изображения? Вернее, объекты этого мира?

То, что мы видим как материальный мир - это лишь очень небольшая (и конечная) часть универсума.

** Сколько граней?

*** Вниз по лестнице размерности

Вернемся теперь к вопросу о количестве 3х-мерных граней и вообще разберемся с гранями. Задумывались ли вы когда-нибудь над тем, что из себя представляет 1-мерный аналог куба? Будем спускаться постепенно: 2х-мерный аналог – это, как было уже сказано квадрат, это может быть показано, например, проекционным способом: найдется такой ракурс на куб, когда мы видим всего лишь квадрат – 3-е измерение теряется в изображении. Точно также если проецировать квадрат на прямую (разумеется, находящуюся в одной плоскости с ним, 3-его измерения-то нет в плоском мире), то в общем случае он будет давать конструкцию из 4 точек. Но можно подобрать и такой ракурс, что останется всего 3 точки. Апофеозом этой проекционной изворотливости будет ракурс, при котором в проекции останется всего 2 точки и 1 отрезок. Который и является полным 2х-мерным вырождением квадрата – на нем исчезают последние остатки 2-го измерения в квадрате.

*** Теперь обратно

Будем теперь двигаться в обратном направлении: допустим, мы хотим отрезок превратить в квадрат - как к этому подступиться? Поможет нам в этом деле следующее рассуждение: вообще говоря, отрезок есть часть 1-мерного мира (прямой), отделенная (отграниченная) от остальной его части 0-мерными гранями – концами отрезка. Таким образом, у отрезка и грани, и вершины суть одно. Как известно их всего 2, так как измерение простирается в 2-х направлениях – вперед и назад. Когда из 1-мерного мы попадаем в мир 2х-мерный, оказывается, что граней нужно уже не 2, а 2*2 – по 2 на каждое измерение. И притом, что они становятся отрезками, так как в 2х-мерном мире невозможно отграничиться точками. Таким образом, мы получаем квадрат, 2х-мерный аналог куба. У квадрата и грани и ребра суть одно.

После этих рассуждений становится, наконец, понятно, что у гиперкуба должно быть не 6, а 8= 2*4 граней, причем они должны быть 3х-мерными. Так как в 4х-мерном мире отграничиться по измерению уже невозможно обычными в 3х-мерном мире 2х-мерными гранями.

** Сворачиваем развертку

Итак, с разверткой гиперкуба теперь все ясно, остается вопрос, как её свернуть в гиперкуб. Выше уже было сказано, что 3х-мерную развертку гиперкуба не удается свернуть в 3х-мерном мире. Но, быть может, это удастся сделать, допустив искажения? Подобно тому, как это происходит при 2х-мерном изображении куба? Ведь и при этом мы имеем сворачивание 2х-мерной развертки куба в 2х-мерном же пространстве. Что и удается сделать, но при допуске искажений: квадраты (в общем случае) превращаются в параллелограммы (потому что параллельные прямые в любой проекции параллельные) (рис.1).

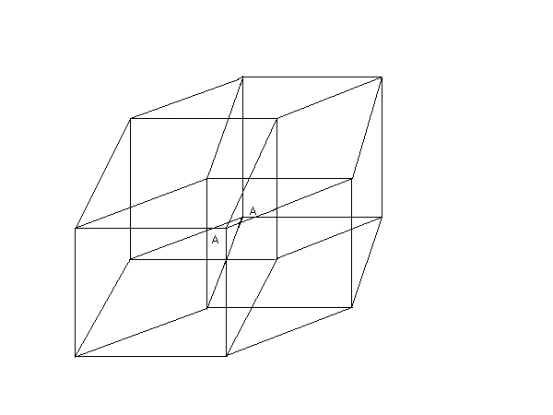
Рис.1 Модель гиперкуба

*** Свойства модели

Но в некоторых случаях (при сборке развертки) квадраты превращаются в ромбы. Это и произошло в моей проекции-модели. Поскольку для моделирования гиперкуба у меня были в распоряжении только равные ребра (в виде спичек), то и получилась несколько неудачная модель. В которой 2 вершины (видимая A и оппозитная ей невидимая A, см. рис.1) слились.

Про гиперкуб и слияние разверток

Дело не только в ромбах, но и в углах между ними. Если применить диметрию для куба, то слияние разверток тоже получится, но огибающей проекции будет уже не правильный 6-угольник.

Кстати, а для гиперкуба огибающей модели будет 8-угольник. И лучше даже правильный?

*** Внутреннее пространство гиперкуба

Из-за слияния вершин модели и создалось ощущение отсутствия внутреннего пространства гиперкуба – развертка как бы схлопулась в некую 4х-мерную точку.

Вообще понятие «внутри» в гипермире какое-то специфическое, как я уже говорил. Оно несколько не по зубам нашему 3х-мерному сознанию. Быть внутри 3х-мерной грани гиперкуба – это нам еще понятно. Но что означает быть внутри гиперкуба? Дело в том, что в одну точку даже 3х-мерного изображения гиперкуба попадает множество точек, находящихся внутри гиперкуба.

По-видимому, здесь (чтобы получить изображение внутренней точки гиперкуба) помогут некие сечения и, возможно, 3х-мерные.

** Другой путь

Можно, конечно, идти другим путем - начать с 4х-мерной СК. В самом деле, разве мы не можем (пусть даже и 3х-мерном мире) из одной точки испустить 4 луча? Можем, и даже более того: мы можем испустить их под равными углами друг к другу, в точности так, как расположены 4 атома водорода по отношению к атому углерода в молекуле метана.(этот же прием применен в начертательной геометрии в случае изометрической проекции, в пику диметрической) Теперь остается только превратить каждый координатный луч в прямую (правда, при этом равенство всех углов потеряется), и мы получим идеальную 4х-мерную СК координат в 3х-мерном мире. А точнее – ее идеальную модель. После этого остается только провести на каждой оси (желательно) перпедикулярные ей (3х-мерные) грани и дождаться их (взаимного, конечно) пересечения. Нет, не по прямым! Это только плоскости пересекаются по прямым. А гиперплоскости (то есть 3х-мерные) пересекаются по плоскостям!

Это и имеет место на нашей модели гиперкуба.

* Сравнение гиперкуба с кубом

3х-мерный куб:

граней= 6= 2*3, ребер= 4*6/2 (всего в кубе), ребер (в грани)= 4, вершин= 8 (всего), вершин (в грани)= 4.

4х-мерный куб:

3х-мерных граней- 2*4= 8, ребер= 32, ребер (в 3х-мерной грани)= 12, вершин= 16, 2х-мерных граней= 24.

Объем 4х-мерного куба равен объему 3-х непересекающихся составляющих его кубов= 3*2^3= 24, что неправильно. Так, объем 4х-мерного куба (c ребром 2)= 2^4= 16

Интересное замечание: 3х-мерная модель 4х-мерного куба также является правильным многогранником (что все его грани конгруэнтны), с тем лишь исключением, что что они не являются правильными многогранниками.

* Несколько соображений о платоновых телах

1)тетраэдр дуален сам себе (4 грани-> 4 вершины)

2)куб дуален октаэдру (6 граней, 8 вершин у куба, и наоборот у октаэдра)

3)додекаэдр дуален икосаэдру (12 граней, 20 вершин у додекаэдра, и наоборот у икосаэдра)

* Природа углов, 4х-мерная сфера

Плоский угол соответствует делению длины окружности, 3-мерный (телесный) угол соответствует делению площади поверхности 3хмерной сферы. 4х-мерный угол соответствует делению объема (не площади!) 3х-мерной поверхности 4х-мерной сферы.

Вывод: нужно вводить определения:

1)(n-1)-ой поверхности n-мерной фигуры;

2)(n-2)-ой поверхности n-мерной фигуры и т.д.

Если n>=4.

Если x^2+ y^2+ z^2= R^2 – это уравнение 3х-мерной сферы, то каково уравнение, соответствующей ей (n-1)-ой поверхности? Чтобы по нему можно было легко определить ее площадь.

Уравнение 2х-мерной поверхности сферы совпадает с уравнением самой сферы, не совпадают только способы его обработки при вычислении объема и площади поверхности – типы интегралов разные. Намного интереснее (этот вопрос) для 4х-мерной сферы.

Уравнение 4х-мерной сферы, очевидно

x^2+ y^2+ z^2+ t^2= R^2

* 4-хмерный аналог многогранников

Дальнейшие эксперименты с 4х-мерным пространством

(3х-мерное моделирование 4х-мерных фигур) показали, что в ряде случаев аналогом треугольника является не тетраэдр, а 4х-гранная пирамида. Это зависит от того, с какой плоской фигурой он сопрягался в той 3х-мерной фигуре, 4х-мерный аналог которой мы пытаемся построить (а точнее – 3х-мерную модель этого 4х-мерного аналога).

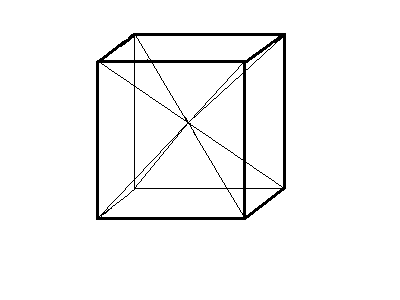
Рис.2. 4х-мерный аналог правильной 4-угольной пирамиды

Еще один интересный вопрос: сколько у выстраиваемой 4х-мерной фигуры будет вершин, ребер, 2х-мерных и 3х-мерных граней? Как вычислить объем 4х-мерной фигуры?

Например, что будет 3х-мерным аналогом 5-угольника? Вроде бы, не существует такой фигуры.=> не существует 4х-мерного аналога 5-угольной пирамиды?

Как вообще находить аналог фигур, построенных из квадратов, прямоугольников и сферы?

* Общие размышления об аналогичности

Идея аналогичности 3х- и 4х-мерных фигур в целом неправомерна и имеет шанс быть развитой только для 1)многогранников – поскольку для них аналитические выражения чрезвычайно громоздки, и то не для всех); 2)для симметричных фигур.

Действительно, как от произвольного уравнения с 3-мя переменными перейти к аналогичному ему уравнению с 4-мя переменными?

Для сферы это сделать легко, поскольку её уравнении имеет место полная симметрия переменных (то есть в результате любых перестановок переменных получается исходное выражение)(то есть в результате любых перестановок переменных получается уравнение, эквивалентное исходному.

Еще один пример такого уравнения:

x*^y^2*z^2= R^6 (или просто x*y*z= R^3)

Аналог его найти просто: x*y*z*t= R^4

То же самое – переход от 3х-мерной плоскости к 4х-мерной:

x+y+z= R => x+y+z+t= R.

Но каков, к примеру, 4х-мерный аналог плоскости

a*x+ b*y+ c*z= d?

Какой коэффициент ставить перед t в уравнении аналога? Если бы, например, было так:

x+ a*y+ a^2*z= b,

то аналог нашелся бы легко:

x+ a*y+ a^2*z+ a^3*t= b,

поскольку коэффициенты при переменных представляют из себя геометрическую прогрессию. И тем не менее, это – частный аналог, так как чисто теоретически всегда может найтись всегда может найтись следующий член ряда, разрушающий созданную для него (или до него?) гипотезу о закономерности.

* Проект на будущее

Не пора ли начать разрабатывать тему «Путешествия в 4-ое измерение»? В неё обязательно включить главу о симметрии. И в ней упомянуть, что при переходе из планиметрии к стереометрии центральная симметрия превращается в осевую, осевая – в плоскостную, но возникает еще и 3х-мерная центральная симметрия. И при этом все это (до сих пор) не имеет (по традиции?) определений. А имеет только примеры (случаев).

Часть 2

Многогранники и платоновы тела

* Основы аналогии наращивания измерений

** Многообразия

Пространства пересекаются не по прямой, а по плоскости.

Признак параллельности пространств?

** Сфера и многогранники

*** Аналитичность и изобразительность

План "Путешествия в 4-ое измерение"

1.Гиперкуб

2.Гиперсфера

(14.06 3.Гипермногограннники)

Гиперсферу проще отображать аналитически, в т.ч. все производные (и компоненты?) от нее - ее поверхность, площадь поверхности и т.п.

А если от гиперсферы, то сначала её 3х-мерную поверхность.

*** Порядок симметрии

Но сфера - это как бы симметрия бесконечного порядка (центральная), а также осевая.

В кубе имеет место только симметрия дискретного порядка (совпадающая с симметрией СК) Не таковы многогранники вообще. Поскольку в них симметрия тоже дискретная, но она не совпадает с симметрией СК. Так, в тетраэдре имеет место пространственная (а не плоскостная) центральная симметрия 4-го порядка. В октаэдре - (такая же) симметрия 8-го порядка, и т.д. по количеству граней (14.06 А почему не по количеству вершин?)

И здесь возникает вопрос: если у просто платоновых тел грани есть 3х, 4х и 5х-угольники, причем для 3х-угольников есть даже 3 платоновых тела (4, 8 и 20-эдры), то о чем это говорит?

*** Аналитический способ

Что мы можем делать в аналитике?

1.проводить прямые, плоскости и даже пространства

2.проводить углы между ними, как между прямыми, так и плоскостями (телесные), но так же и между пространствами. (4х-мерные телесные углы)

То же самое касается и площадей, объемов и т.п. 4х-мерный объем - это не 3х-мерный.

Но поверхность фигуры, имеющей 4х-мерный объем, имеет 3х-мерную площадь (=объем), и т.д.

* Многогранники

** Размножение граней

*** Тетраэдр

Очень давно я придумал перпендикулярно (осям симметрии) срезать вершины правильных многогранников. Получались некие полуправильные многогранники. Например, из тетраэдра получался многогранник, поверхность которого состояла не только из треугольников, но и из 6-угольников (в них превращались исходные грани)(рис.), по мере увеличения глубины срезания превращавшиеся опять в 3-угольники. В итоге имеем октаэдр.(Да нет, ошибка! Тетраэдр это. 14.06 1-ый раз был прав: все-таки октаэдр. Еще одну вершину не разглядел.)(рис.)

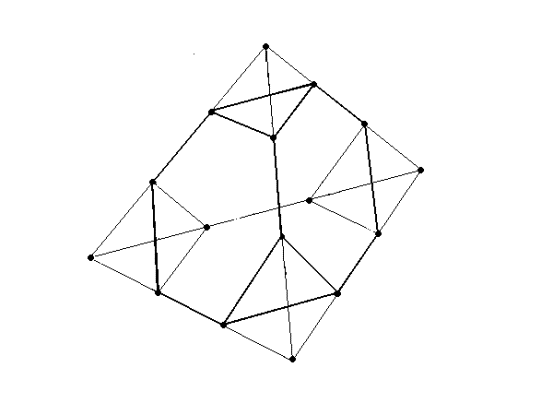
Рис.3. Тетраэдр со срезанными вершинами

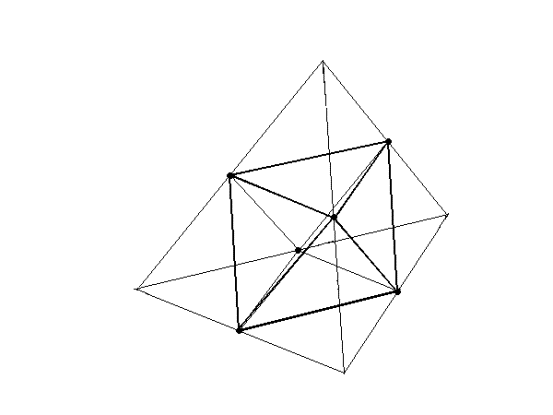
Рис.4 Превращение тетраэдра в октаэдр.

*** Куб, пример сверхглубокого срезания

Теперь начинаем (также) срезать вершины у куба (гексаэдра). В результате в местах среза образуются 3-угольники, а бывшие грани превращаются в 8-угольники. При увеличении глубины среза 8-угольники опять превращаются в 4-угольники (квадраты)

При дальнейшем увеличении глубины среза 3-угольники превращаются в 6-угольники (смыкающиеся между собой по вновь появившимся ребрам), а квадраты - остаются квадратами. (рис.)Пока не?..

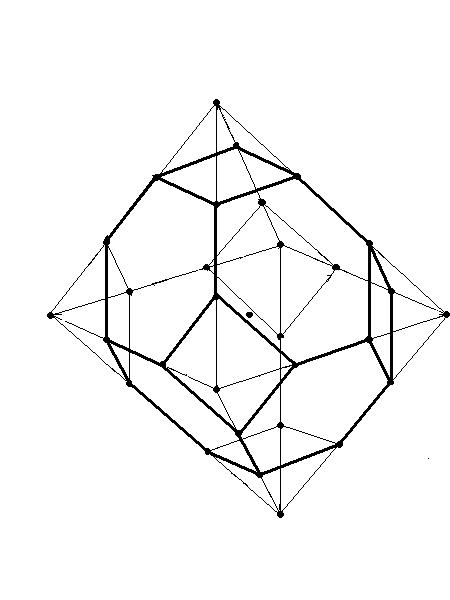
Рис.5. Сверхглубокое срезание вершин куба

*** Додекаэдр и куб

При срезании вершин 12-эдра (до упора) он превращается в 20-эдр.

Куб превращается в 8-эдр.

(16.06 а вот это (и 1-ое и 2-ое) – ошибка. Но главное – не этот факт сам по себе, а природа его получения)

Пока (при продолжении увеличения глубины срезания) не сойдется в точку. (см. рис. В блокноте, стр. с красным углом)

(и это – ошибка. При увеличении глубины срезания куб не превращается в точку, и это подсказывает последний рисунок.)

Тетраэдр превращается сам в себя.

(17.06 И это, как мы видели выше - ошибка. А причина известна - срезание вершин (оно же вписывание между ребер) перепутано с вписыванием между гранями)

Так что фундаментальный здесь вопрос - это вопрос о симметрии. Который очень стар. Но также и очень неразвит.

(найти материал по следам занятий с С-ом, про симметрию и интерсимметрию и симметричные (инвариантные?) преобразования)

*** 2-ой порядок срезания - приближение к сфере

Еще не зафиксировал одну идею: предположим, срезали вершины у куба. Но не до упора. А почему бы не срезать по 2-ому порядку? И т.д., для увеличения порядка симметрии.

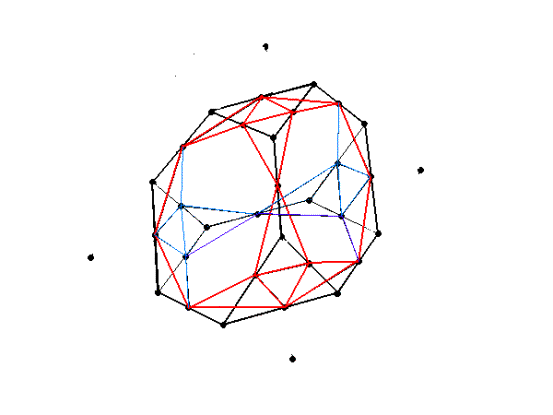
Рис.6. Срезанный по 2-ому порядку тетраэдр

До того

Срезание вершин у многогранников (при рекурсивном срезании) - это способ построения более многогранных многогранников. И более разнообразный, чем на плоскости.

Рефлексия

Все-таки я путаю вопросы: 1)о 4х-мерной аналогичности; 2)об образовании многогранников. Так что, получается уже 2 статьи?

(связка через приближение к сфере)

У сферы нет ни граней, ни вершин, ни ребер. Это результат перехода в бесконечность. Самая малая поверхность по сравнению со сферой - у 4-эдра. Самая близкая, по-видимому, у 20-эдра. То есть: чем больше граней, тем ближе площадь поверхности к поверхности сферы.

Модель же 4х-мерной сферы, как и 3х-мерной, по-видимому, ничем не отличается от окружности. Таким образом, ничто в ней не говорит о её структуре. Структура может быть выявлена только за счет сечений. Пересекая 3х-мерную сферу плоскостью (под любыми углами), мы получаем окружности. Подобно этому, пересекая 4х-мерную сферу 3х-мерными пространствами

(в связи с этим возникает вопрос об угле между 3х-мерными пространствами),

мы будем получать 3х-мерные сферы. Пересекая её плоскостями, будем получать окружности.

Кстати, отрезок аналогичен не только кубу. Отрезок также есть 1-мерный аналог сферы. Это следует из того, что пересечение сферы прямой дает отрезок – 1-мерный аналог сферы. А также из того, что проекция окружности на прямую есть отрезок. Но если быть точным, даже не отрезок, а пару точек. Это круг дает отрезок.

*** Промежуточная фигура

Октаэдр срезанный (до упора) аналогичен срезанному кубу (рис.).(14.06 то есть этот многогранник есть нечто среднее между кубом и и октаэдром – октаэдрокуб или, что то же самое, кубооктаэдр.)

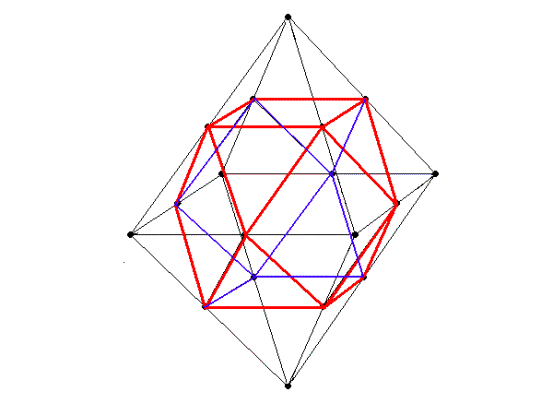
Рис.7. Срезанный до упора октаэдр

Срезанный до упора 20-эдр дает срезанный до упора 12-эдр (икосадодекаэдр).

* Аналоги многоугольников

«И здесь возникает вопрос: если у просто платоновых тел грани есть 3х, 4х и 5х-угольники, причем для 3х-угольников есть даже 3 платоновых тела (4, 8 и 20-эдры), то о чем это говорит?»

** Квадрат и треугольник

Но я пропустил следующий момент: если 3х-мерным аналогом квадрата является куб, то таким же аналогом 3-угольника является тетраэдр?

Да, точно: если равномерно распустить 3 луча на плоскости, то получатся оси симметрии 3-угольника, а в пространстве (но уже 4!) - оси симметрии тетраэдра.

Но почему от 3 осей мы переходим к 4? Не потому ли, что от фигуры 3-угольника мы переходим к 3-угольнику-грани?

** 5-угольник

Но как тогда нам быть с правильным 5-угольником? Ведь 3х-мерный многогранник из 5-угольных граней есть додекаэдр и содержит 12 граней? Но это еще цветочки: есть и такие многоугольники, которые вообще не представлены в платоновых телах.

** Многоугольники в платоновых телах

По-видимому, 5 платоновых тел связаны с простым отображением синусов этих углов через радианы. Простое отображение 2*Pi/5 неизвестно широкой публике. Но не достаточно ли посмотреть на решения уравнений про золотую середину? -это ведь и есть sqrt(5)?

1/x= x/(1-x) => x^2+x-1=0 => D=5 => x1=(-1+sqrt(5))/2, x2=(-1-sqrt(5))/2

Нет, это не дает связи с 5-ым измерением. Даже на плоскости. (14.06 Впрочем, проверка на косинусе дает иное: 2*cos(2*Pi/5)= x1! Значит, все-таки каноническое (с помощью циркуля и линейки) построение пятиугольника подтверждается)

** Природа платоновых тел

Нужно найти способ вычислять углы между векторами 4х-мерном пространстве. И делить поверхность 4х-мерной сферы на 5 равных частей= испустить 5 лучей из одной точки, равноотстоящих.

На промежуточные количества частей сферы поделить можно, но это тогда будет равняться по площади, а не по форме граней.

Но отсюда, как кажется, ведет начало с простыми числами (14.06 А не с числами Фибоначчи?)

И их отображениями (в том числе в виде необыкновенных дробей)

** 6-угольник

Но я, кажется, отвлекся от проблемы 4х-мерных аналогов. Итак, 4х-мерного аналога 5-угольника нет, поскольку нет и 3х-мерного. Но как быть насчет 6-угольника? Ведь правильный 6-граннник существует.

*** Критерий аналогичности

Но мы не следовали раньше этому критерию аналогичности (количество граней= количеству ребер), иначе 4-эдр был бы аналогичен квадрату, а не 3-угольнику. Так каков наш критерий аналогичности? Мы до сих пор его не сформулировали. (14.06 Не потому ли, что это не простая аналогичность, но с (обязательным) повышением размерности. Что само по себе уже нарушает аналогичность.)

* Многогранники

** Природа платоновых тел

*** n-секция угла

Куб получается в результате деления телесного угла на 6 равных частей, тетраэдр - на 4.

Интересно, а можно поделить телесный (развернутый) угол на 5 равных частей? Формально - да, но отобразить это (результат) - нет, т.к. в противном случае существовал бы многогранник с 5 вершинами и дуальный ему с 5 гранями.

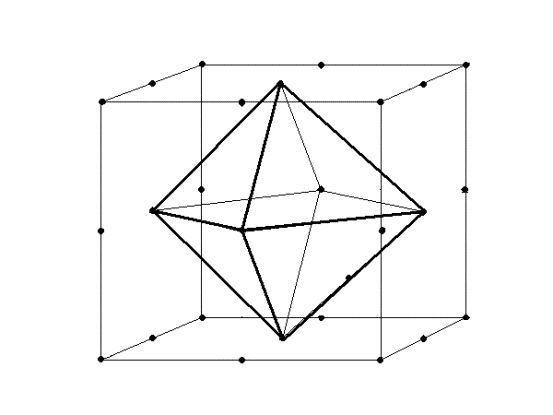
Рис.8. Пример дуальности: вписанный в куб октаэдр

Задача порождения правильных многогранников сводится к задаче n-секции развернутого телесного угла. (который равен 4*Pi).

(По аналогии

Развернутый 4х-мерный телесный угол, очевидно, равен (4-1)*2*Pi.)

Тогда как n-секция плоского угла разрешима при любом n, то n-секция телесного угла, по-видимому, нет. Нужно расположить на поверхности сферы n равноудаленных друг от друга точек. Итак, в 3х-мерном мире получается 3*n неизвестных и n*(n-1)/2+1 уравнений.

*** Которые соседи?

Нет, равноудаление проверяется не для всех, а только для смежных= соседей. На окружности их будет всегда 2, а на сфере? Например, для 4-эдрической конфигурации для каждой вершины есть 3 соседа (и несоседей нет). В 6-эдрической конфигурации у вершины тоже 3 соседа, но несоседей уже 4. В 8-эдре у вершины 4 соседа, а несоседей (у каждой вершины) -1. В 12-эдре у вершины 3 соседа, и (20-4) несоседей. В 20-эдре: соседей - 5, несоседей - (12-6).

Как отыскиваются, из какого уравнения, все эти конфигурации?

*** Базовые конфигурации

В 3х-угольнике плоской конфигурации расстояния все со всеми, то же самое и в 4-эдрической 3х-мерной. Так что это базовые конфигурации. (15.06 И они аналогичны!)

(15.06 А какова базовая конфигурация в 4х-мерном мире?)

*** Периодическая развертка

Задача сводится к построению (периодической) развертки, которая замкнется в пространстве данной размерности. (что-то здесь попахивает фракталами, пусть и не 1-членными)

И эта задача не аналогична периодическому покрытию пространства данной размерности многоугольниками или многогранниками.

(связка-переход через сферу)

А что если изучать многогранные структуры, вписывающиеся в эллипс? Или эллипсоид? Регбисты мне не дадут соврать.

* Многогранники

** Аналоги

*** Тетраэдр

Развертка тетраэдра - это тетраэдр, на каждую грань которого прилеплено по такому же тетраэдру. Остается теперь эту развертку свернуть. В итоге получится следующее:

Рис.9. 4х-мерный тетраэдр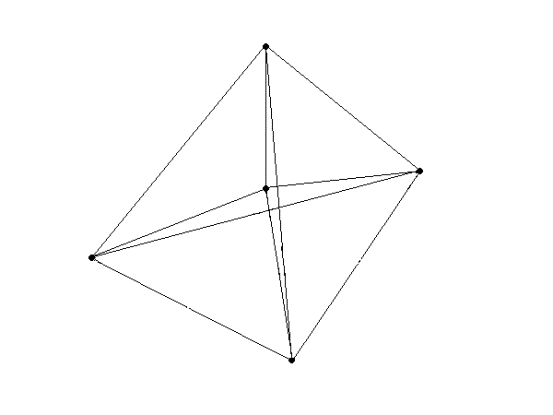

В таком случае 4х-мерный аналог 8-эдра тоже найдется просто:

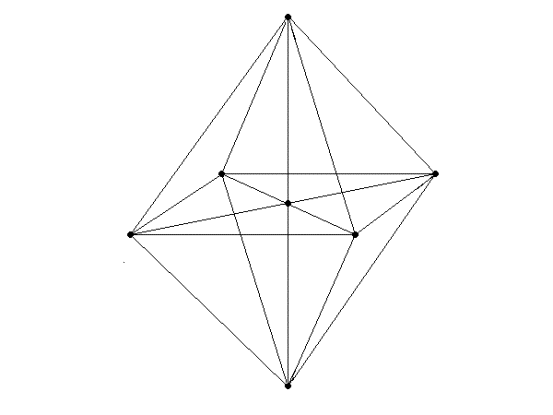
Рис.10. 4х-мерный октаэдр

Но в том-то и дело, что фигуры эти не соответствуют нашему принципу аналогичности. Ведь ранее было показано, что у 4х-мерного куба не 6, а 8 3х-мерных граней. Значит, у 4х-мерного 4-эдра их >4. Но сколько?

5,6? Тот же самый вопрос и относительно 4х-мерного 8-эдра. Может, эти 4х-мерные аналоги просто отсутствуют?

*** Ущербная развертка?

Добавляя к квадрату по квадрату (с каждого ребра) и сворачивая такую конструкцию, получаем неполноценный куб, без одной грани. Она и замкнет куб, образуя его внутреннее пространство. Но куда вписать 5-ый 4-эдр в 4х-мерном аналоге 4-эдра?

Идея: 5 4-эдров получится, если вписать в 4-эдр в 4-эдр (рис.) или до упора обрезать. Но какая из этих структур есть 4х-мерный аналог 4-эдра? Скорее всего, 2-ая. Потому что в 1-ой получается не 5 4-эдров, а нечто иное, я еще не совсем понял, что.

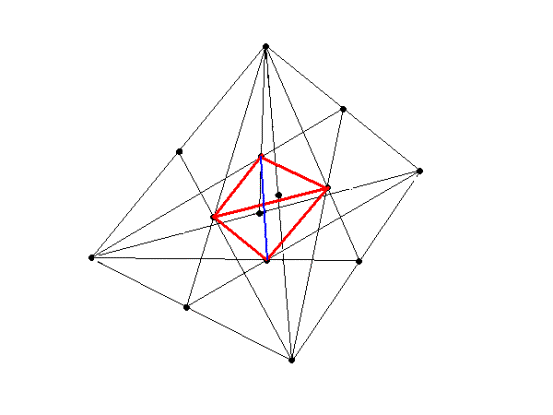
Рис.11. Тетраэдр, вписанный в тетраэдр

Стоп, но это (рис. Срезанный до упора тетраэдр) и есть та самая развертка, о которой я уже говорил! Но ведь её надо ещё свернуть! Вот и получится то, что я уже показывал (рис. 4х-мерный тетраэдр). В этой конфигурации и есть 5 тетраэдров, один из них – наружный. Его-то я и не досчитался.

(17.06 Кажется, это еще одна ошибка. Ибо в срезанном до упора тетраэдре в ядре не тетраэдр, а октаэдр!)

(19.06 что же касается «тетраэдра в тетраэдре», то высоты периферийных тетраэдров в нем явно надо уменьшать. Что мы и сделали (см. рис. Развертка гипертетраэдра))

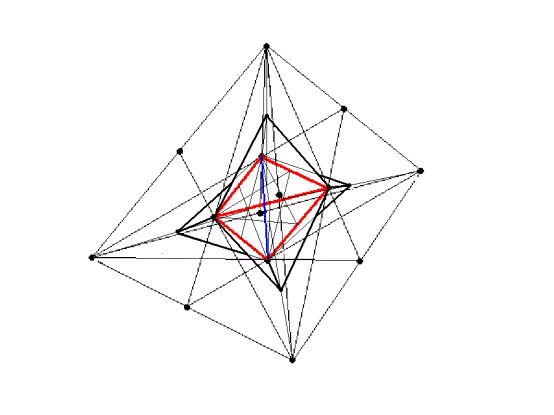
Рис.12 Развертка гипертетраэдра