[ Привет, физматика! ] [ Что нового на сайте ] [ Разобраться  в теории ] [ Если не решается задача ] [ Тесты на понятливость ] [ Ну очень трудные задачи ] [ Короткие заметки ] [ Статьи ] [ Форумы ] [ О нас пишут ]

 

Трактат о гиперболе и ее родственных связях

 

 

В школе нам впервые становится известно о функции обратной пропорциональности y= k/x и о ее графике – гиперболе. Но в вузе, в курсе аналитической геометрии, нам почему-то рассказывают про другую гиперболу – которой (в простейшем случае) соответствует уравнение x^2- y^2= k.

Но как же так, уравнения разные, а кривые одинаковые? Постараемся разобраться в этом вопросе.

 

Некогда довелось мне взяться за решение уравнений электростатического поля. Известно, что их всего два:

(1)div(D)=r  

(2)rot(E)=0,

где r(x,y,z)- объемная плотность заряда в пространстве.

Как я их решал и причем здесь гиперболы – об этом вы и узнаете, перелистнув страницу.

 

Содержание

 

Изначальные гиперболы. Сложение гипербол. Умножение гипербол. “Плохое” семейство (4-го порядка) и способы его улучшения. Преобразования гипербол (инвариантность?). Ни «рыба», ни «мясо» (гиперболы 3-его порядка). Разборки с инвариантностью. Добрались до 5-го порядка. Колебания в полярной системе координат. Об одном странном источнике гипербол: (Электростатические уравнения. Скандал о граничных условиях,  и не только. Симбиоз общего с классическим – как он достигается? . Один способ частного решения и что он дает).

 

* Изначальные гиперболы

 

В школе нам впервые становится известно о функции обратной пропорциональности y= k/x (1) и о ее графике – гиперболе. Но в вузе, в курсе аналитической геометрии, нам почему-то рассказывают про другую гиперболу – которой (в простейшем случае) соответствует уравнение x^2- y^2= k (2).

Но как же так, уравнения разные, а кривые одинаковые? Постараемся разобраться в этом вопросе.

Прежде всего преобразуем уравнение (1)к виду xy=k (1.1) и сравним с (2). Мы видим, что правая часть этих уравнений – константа. Это обстоятельство наводит на идею отображать на одном графике сразу все семейство гипербол данного класса. Вот так:

 

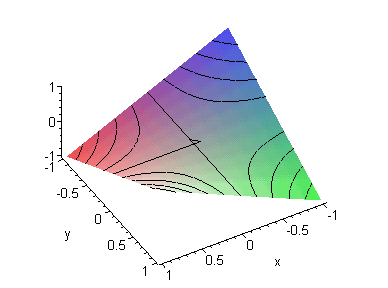
Рис.1. Семейство гипербол класса z=xy

 

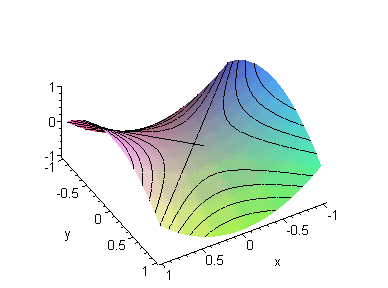
Рис.2. Семейство гипербол класса z=x^2-y^2

 

Из этих двух графиков видно, что изображенные на них кривые действительно схожи.

 

(И даже более того: 2-ая получается из 1-ой при повороте (по часовой стрелке) относительно начала СК на 45 градусов.)

 

Мы видим также, что в обоих уравнениях левая часть есть многочлен 2-ой степени от 2-х переменных. Поэтому проверим, а не дает ли такой же график сумма x^2+xy-y^2?

 

* Сложение гипербол

 

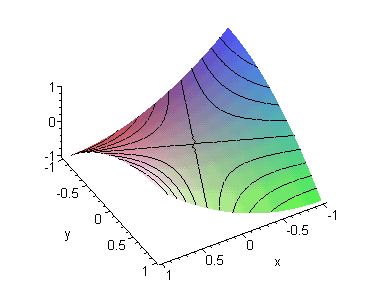
Рис.3. Гиперболы x^2+xy-y^2

 

Наша гипотеза подтвердилась. Действительно, получается новое семейство гипербол. Но теперь уже повернутых относительно гипербол xy где-то на угол 45/2. То есть получается среднее положение между гиперболами xy и x^2-y^2. Подтверждает это предположение рис.3а.

Разумеется, после идеи суммирования гипербол приходит идея их вычитания.

Рис.3а. Директрисы гипербол x^2+xy-y^2

 

Но эту идею можно реализовать проще – достаточно рассмотреть, что получится, если умножить функцию гиперболы на –1. Разумеется, тоже гипербола! Но только там, где у нее была отрицательная область будет положительная, и наоборот.

 

Но оставим этот вопрос на потом (так как за ним видится объемное продолжение). А сейчас зададимся следующим: если при суммировании мы получаем гиперболы, то, быть может, их же получим и при умножении?

 

* Умножение гипербол

 

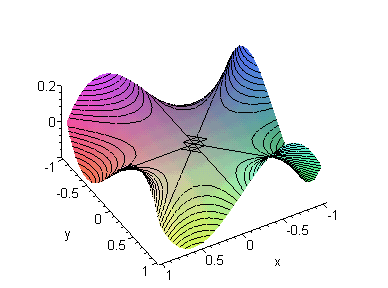
Рис.4. Гиперболы класса xy*(x^2-y^2)

 

Получили очень интересный результат – гиперболу с 4-мя директрисами. Преобразуя xy*(x^2-y^2) в x^3*y-x*y^3, замечаем, что и многочлен-то мы уже имеем не 2-ой, а 4-ой степени! О чем это говорит? Что количество директрис гиперболы равно степени соответствующего ей многочлена.

* “Плохенькое” семейство и способы его улучшения

 

А что если сконструировать другую гиперболу 4-ого порядка и на ней проверить эту гипотезу? Если 1-ую мы сконструировали перемножением двух гипербол 2-го порядка, то как сконструировать новую? Ответить на этот вопрос мы сможем, если обратим внимание на специфическое устройство многочлена x^3*y-x*y^3. А именно, он имеет следующий вид: x^3*y^(4-3)- x^(3-2)*y^(4-3+2). По этому же образцу строится и другой многочлен: x^4- x^2*y^2+ y^4. Но ему соответствует какое-то “плохенькое” семейство гипербол (рис.5).

 

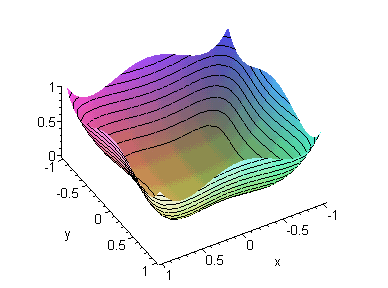
Рис.5. “Гиперболы” класса x^4- x^2*y^2+ y^4

 

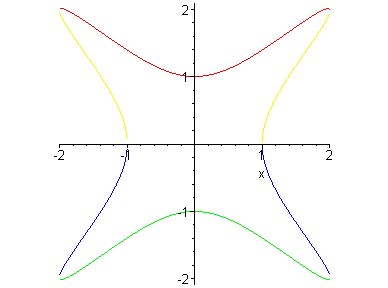
Рис.5а. Изотопы “гиперболы” x^4-31/16*x^2*y^2+y^4

 

А чем оно, собственно, плохо?

Тем, что совсем не имеет директрис. Каким же образом исправить это положение, как же возвратить директрисы? Наверно, что для этого надо изменить удельный вклад разных составляющих многочлена, и в первую очередь обратить внимание на старшие степени, уменьшив их “вес”. Например, так: x^4/2- x^2*y^2+ y^4/2. Что ж, есть результат – появились директрисы (рис 5.1а), но правда всего 2.

 

Рис.5.1а. Директрисы гипербол x^4/2- x^2*y^2+ y^4/2

 

А что если усилить эффект, следующим образом: x^4/4- x^2*y^2+ y^4/4? Да, действительно получилось – появились все 4 директрисы (рис.5.2а).

 

 

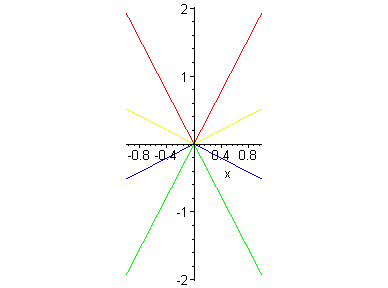
Рис.5.2а. Директрисы гипербол x^4/4- x^2*y^2+ y^4/4

 

Но все-таки до идеала далеко – между директрисами разные углы. Настоящий идеал гиперболы (с равными углами), как ни странно, получается для многочлена x^4/4!- x^2/2!*y^2/2!+ y^4/4 (рис.6).

 

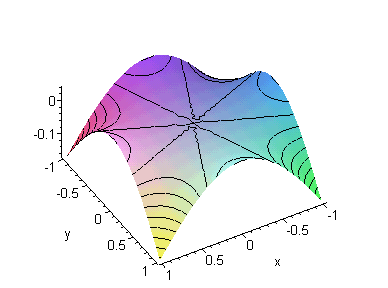
Рис.6. Гиперболы класса x^4/4!- x^2/2!*y^2/2!+ y^4/4!

 

Единственное (на данный момент), но весьма нестрогое объяснение этому дает то обстоятельство, что степенное разложение экспоненты выглядит так:

 

Где 6=3!, 24=4!, 120=5! Вот откуда факториалы к нам идут. (прошу учесть: в предыдущем предложении знак ! – это вовсе не восклицательный)

Таким образом, с помощью деления на факториалы показателей степеней  удалось сбалансировать гиперболы разных порядков. Кстати, и при суммировании разных гипербол 2-го порядка (xy и x^2-y^2) тоже получается несбалансированный тип гиперболы. Он выдает себя тем, что у него углы не равные. Уравнять углы удается только после трансформирования x^2-y^2 в x^2/2!-y^2/2!

 

* Преобразования гипербол (инвариантность?)

 

*** Инверсия

Теперь возвращаюсь к теме инвертирования гипербол. Начало по этой теме уже сказано: если умножить функцию гиперболы на –1 получится тоже гипербола! Но только там, где у нее была отрицательная область будет положительная, и наоборот. Это эквивалентно, для гиперболы xy,  повороту на 90 радусов, как по, так и против часовой стрелки. Ведь данная гипербола имеет центральную симметрию 2-го порядка – при повороте на угол 180 градусов она переходит сама в себя. А при повороте на 90 градусов она переходит в свою противофазу.

 

*** Симметрия, осевая и центральная

Применяя инверсию к гиперболе x^2- y^2, увидим, что не только переходит в свою противофазу, но и в осесимметричную себе форму, так как –x^2+y^2 получается из x^2- y^2 не только за счет умножения на “-1”, но за счет подстановки y=x. Что соответствует преобразованию в осесимметричную форму, то есть повороту на 180 градусов не в плоскости симметрии, а относительно оси, лежащей в плоскости симметрии и по результату совпадает с поворотом в плоскости симметрии на 90 градусов. Но только в данном случае. Ведь нет же такого для гипербол класса xy.

 

* Ни «рыба», ни «мясо» (гиперболы 3-его порядка)

 

Итак, если удалось построить гиперболы 4-го порядка, то почему не попробовать это для 3-его порядка? Тем более, что алгоритм известен. В соответствии с ним получаем два многочлена: x^3- x*y^2 и x*y^2- x^3. Которые, совершенно очевидно, связаны преобразованием инверсии –умножением на –1. (И поэтому x^3- x*y^2 переходят в x*y^2- x^3 за счет поворота на 45 градусов в любом направлении) Это обстоятельство заставляет синтезировать новые

 

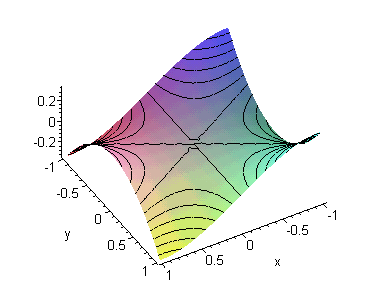
Рис.7.1. Гиперболы x^3/3!- x*y^2/2!

 

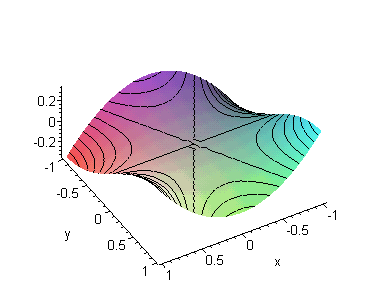
Рис.7.3. Гиперболы y^3/3!- y*x^2/2!

 

варианты: y^3- y*x^2 и y*x^2- y^3. Которые связаны с 1-й парой иным преобразованием: x=y. И которое, как ясно из вышеприведенного, неэквивалентно преобразованию умножением на –1.(это случается только для гипербол четного порядка.) По простой причине: директрисы этих гипербол не совпадают с директрисами 1-ых (x^3/3!- x*y^2/2!). В данном случае они могут быть получены из директрис 1-ых поворотом по часовой стрелке на 30 градусов, то есть угол, вдвое меньший полупериода симметрии 3-го порядка. Или, как ни странно, за счет осевой симметрии относительно прямой x=y, то есть угла 45 градусов.

 

* Разборки с инвариантностью

 

** Пока для 3-его порядка

 

Докажем, что выражение y^3/3!- y*x^2/2! имеет центральную симметрию 3-го порядка, то есть переходит в себя при преобразовании поворота на угол 120 градусов или, что то же самое, инвариантно относительно преобразования {x1= x*cos(fi)- y*sin(fi), y1= x*sin(fi)+ y*cos(fi)}, где fi=2*Pi/3, поэтому cos(fi)= -1/2, sin(fi)= sqrt(3)/2 и итоговое преобразование {x1= -x/2- sqrt(3)/2*y, y1= sqrt(3)/2*x- y/2}. Подставив эти выражения в функцию гипербол A*y^3- y*x^2, получим

По условию инвариантности параметр А должен обеспечивать тождественное равенство этого выражения исходному. Это, как нетрудно определить,  достигается при A=1/3. При другом значении A инвариантность исчезает и функция A*y^3- y*x^2 не является, строго говоря, функцией гиперболы.

 

** А для 4-го – не так-то просто!

 

Ранее, помнится, такой же вопрос (о балансировании слагаемых функции гиперболы с целью уравнения углов между директрисами) возникал для гипербол класса x^4- x^2*y^2+ y^4. Разрешим его с помощью использованного выше метода. Поскольку в данном случае мы имеем дело с симметрией уже 4-го порядка, то поворачивать нужно на угол 90 градусов. Такому повороту соответствует преобразование {x1= 0*x- 1*y, y1= 1*x+ 0*y}=> {x1=-y, y1=x}. Подставив это в исходное выражение A*x^4- B*x^2*y^2+ y^4, получим x^4- B*x^2*y^2+ A*y^4, откуда следует, что A=1, а B может быть любым.

 

*** Трансформации балансирования

Но проверка выше показала, что это неверно: при B=1 получается поверхность вообще без директрис. (напоминающая ската и имеющая звездообразные изотопы (рис.5а). Эта поверхность есть промежуточное состояние между круговым параболоидом (он получается при B=-2) и гиперболоидом.) Точно при B=2 появляется 2 директрисы(y=x, y=-x). Как только параметр B превосходит 2, каждая из этих директрис расщепляется на 2, которые при увеличении B расходятся. Наконец, при B=6 получается сбалансированная гипербола. При дальнейшем увеличении B директрисы в квадрантах продолжают расходиться, теперь уже сходясь на границах между ними.

 

*** Симметрия функции и симметрия директрис

Значит, при проверке на инвариантность допущена какая-то ошибка? Нет, никакой ошибки нет: все вышеперечисленные поверхности действительно имеют симметрию 4-го порядка. А что же касается наличия директрис и их равноотстояния друг от друга – так ведь таких требований (в нашем доказательстве) и не предъявлялось. Это на первый взгляд кажется странным: разве может иметь место симметрия 4-го порядка, если директрисы не равноотстоят друг от друга? Может, потому, что для всех классов рассматриваемых гипербол директрисы, если брать их через одну, все-таки равноотстоят, и причем на угол 90 градусов. Что касается наличия симметрии, то для этого вовсе не требуется налиия директрис.

 

 

* Добрались до 5-го порядка

 

** Погрешности «универсального» метода

 

Поскольку алгоритм конструирования гипербол теперь известен, можно и дальше продолжать процесс конструирования: вот гиперболы 5-го порядка: x^5- x^3*y^2+ x*y^4, x^4*y- x^2*y^3+ y^5, x^3*y^2- x*y^4, x^2*y^3- y^5, x*y^4, а вот – 6-го: x^6- x^4*y^2+ x^2*y^4- y^6, x^5*y- x^3*y^3+ x*y^5, x^4*y^2- x^2*y^4+ y^6, x^3*y^3- x*y^5, x^2*y^4, x*y^5. Но давайте не будем забегать вперед. Что касается гипербол x^5- x^3*y^2+ x*y^4 и x^4*y- x^2*y^3+ y^5, то с ними все в порядке – они имеют 5 директрис и при коэффициентах соответственно 1/5!, 1/3!/2!, 1/1!/4! (для 1-ой гиперболы) – равноотстоящие по углам (рис.8). Но вот насчет x^3*y^2- x*y^4, x^2*y^3- y^5, а тем более x*y^4 возникают некоторые сомнения.

 

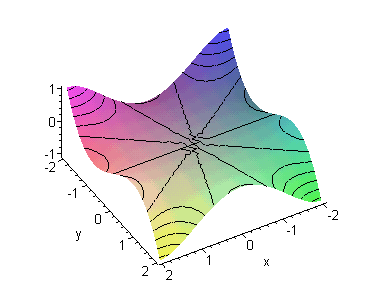
Рис.8. Гиперболы x^5/5!- x^3/3!*y^2/2!+ x*y^4/4!

 

Так как x^3*y^2- x*y^4= x*y^2*(x^2- y^2), то очевидно, что данной гиперболы всего 4 директрисы (x=0, y=0, y=x, y=-x), то есть это псевдогипербола 5-го порядка. Поскольку x^2*y^3- y^5= y^3*(x^2- y^2), то у этой гиперболы всего 3 директрисы (y=0, y=x, y=-x), то есть она вырождена еще больше. Наконец, самая вырожденная гипербола – это x*y^4, поскольку у нее, как нетрудно видеть, всего 2 директрисы (x=0, y=0).

 

** Универсальный Метод

 

Вышеприведенный анализ подсказывает универсальный метод конструирования гипербол с каким угодно множеством директрис. Например, требуется гипербола со следующими директрисами: y=x, y=-x, y=2*x, y=-2*x. Строим выражение(y-x)*(y+x)*(y-2*x)(y+2*x) и раскрываем его: y^4-5*x^2*y^2+4*x^4. Это и есть желаемое семейство гипербол (рис.9).

 

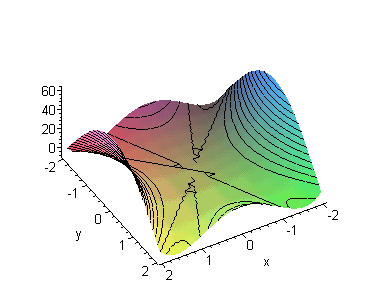
Рис.9. Гиперболы y^4-5*x^2*y^2+4*x^4.

 

*** Со сдвигом фазы

Что же касается сбалансированных гипербол, то их можно тоже сконструировать очень много (с учетом возможности сдвига фаз), следуя такому алгоритму: выбираем начальную фазу, пусть это будет 30 градусов, этому соответствует директриса y=x*sqrt(1/3). Далее выбираем период – пусть это будет 90 градусов (период желательно брать кратным 360 градусам, иначе возможны непредсказуемые последствия). Этому периоду соответствуют следующие преобразования:{x:=-y, y:=x}. Применяя их к уравнению 1-ой директрисы, получаем уравнение 2-ой директрисы: x=-y*sqrt(1/3)=> y=-x*sqrt(3). Далее эти же преобразования применяем к уравнению 2-ой директрисы, в итоге имеем: x=-y*sqrt(3) => y=-x*sqrt(1/3). Это и есть уравнение 3-ей директрисы. Уравнение 4-ой директрисы получится так: x=y*sqrt(1/3) => y=x*sqrt(3). В итоге конструируем функцию гиперболы: (y-x*sqrt(1/3))* (y+x*sqrt(3))* (y-x*sqrt(1/3))* (y-x*sqrt(3)). Остается ее раскрыть, и вот оно, чудо математической мысли: x^4- 10/3*x^2*y^2+ x^4 – гипербола с задаными свойствами.

 

* Колебания в полярной системе координат

 

Приведенные выше рассуждения приводят к следующей мысли: истинные (=сбалансированные) гиперболические поверхности – это некие колебания, но в полярной системе координат. Представим себе, что мы рарезаем гиперболическую поверхность цилиндрической, ось которой совпадает с осью z, что получится? Получится, по-видимому, некое подобие синусоиды. Поэтому все гиперболы очень даже родственны с тригонометрией.

 

Чтобы проверить эту мысль, возьмем для начала гиперболу x^2- y^2 и переведем ее в полярную систему СК: {x=r*cos(f), y=r*sin(f)}. Получим r^2*(cos(f)^2-sin(f)^2)= r^2*cos(2*f). Итак, уравнение семейства гипербол в цилиндрической СК выглядит так: z= r^2*cos(2*f). При r=const (а это и есть сечение цилиндрической поверхностью) мы и получим периодическую функцию с периодом Pi. Аналогично гипербола xy превращается в r^2/2*sin(2*f).

Перейдем теперь к более сложным гиперболам – 3-его порядка. Возьмем гиперболы x^2*y- y^3/3. В полярной СК это будет выглядеть как: r^3*(cos(f)^2*sin(f)- 1/3*sin(f)^3)= r^3*sin(f)*(cos(f)^2- 1/3*sin(f)^2)= r^3*sin(f)*(1-sin(f)^2- 1/3*sin(f)^2)= r^3*sin(f)*(1-4/3* sin(f)^2)= 1/3*r^3*sin(3*f) [Двайт Г.Б. Таблицы интегралов] Нетрудно сообразить, что гипербола x^3-x*y^2 эквивалентна 1/3*r^3*cos(3*f), то есть идет со сдвигом по фазе на +Pi/2.

Не правда ли, обнаружена весьма неожиданная связь?

Испытаем еще для верности класс гипербол 4-го порядка, ранее наиболее многократно упоминаемый: x^4-6*x^2*y^2+y^4. Перевод его в полярную СК дает: r^4*(cos(f)^4- 6*cos(f)^2*sin(f)^2+ sin(f)^4)= r^4*(cos(f)^2*( cos(f)^2-3* sin(f)^2)+ sin(f)^2*(-3*cos(f)^2+ sin(f)^2)= r^4*(cos(f)^2*(1-4*sin(f)^2)+ sin(f)^2*(1- 4*cos(f)^2)= r^4*(cos(f)^2- 4*cos(f)^2*sin(f)^2+ sin(f)^2- 4* cos(f)^2*sin(f)^2)= r^4*(1- 2*sin(2*f)^2)= r^4*cos(4*f). Получили, как и ожидалось, функцию с периодом 2*Pi/4. По-видимому, есть для нее и пара, описываемая выражением r^4*sin(4*f). Которая в декартовой СК выглядит как x^3*y- x*y^3. Заинтересованному читателю предлагаю самостоятельно продолжить эти исследования для гипербол более высоких порядков.

 

* Об одном странном источнике гипербол

 

** Электростатические уравнения

 

Некогда довелось мне взяться за решение уравнений электростатического поля. Известно, что их всего два:

(1)div(D)=r  

(2)rot(E)=0,

где r(x,y,z)- объемная плотность заряда в пространстве

Будем для упрощения рассматриваются такие поля, в которых всюду Ez=0, а также всюду d/dz=0, то есть поле не изменяется вдоль координаты z. В этом случае вышеприведенные уравнения сводятся к

(3)dEx/dx+ dEy/dy=r(x,y)/e,

где e – диэлектрическая проницаемость среды

(4)dEx/dy- dEy/dx=0 => (4а)dEx/dy= dEy/dx

Дифференцируя уравнение (3) по x, получим

(5)d2Ex/dx^2+ d2Ey/dx/dy= 1/e*dr(x,y)/dx

Дифференцируя (4а) по y:

(6)d2Ex/dy^2= d2Ey/dx/dy

Подставляя (6) в (5):

(7)d2Ex/dx^2+ d2Ex/dy^2= 1/e*dr(x,y)/dx

Аналогичное уравнение легко выводится и для Ey:

(8)d2Ey/dx^2+ d2Ey/dy^2= 1/e*dr(x,y)/dy

Таким образом, получены два электростатических уравнения, которые в совокупности равносильны системе уравнений (3+4), но обладают одной важной упрощающей особенностью – они независимы, то есть искомые функции (Ex и  Ey) в них разделены. К тому же они абсолютно аналогичны по форме. Поэтому достаточно рассмотреть решения только одного из них.

 

 

** Скандал о граничных условиях,  и не только

 

*** Общее решение, простейший случай

Начнем с простейшего случая: заряд вдоль оси x распределен равномерно, тогда dr/dx=0 и уравнение сводится к

(9)d2Ex/dx^2+ d2Ex/dy^2= 0

Известно, что данное уравнение имеет общее аналитическое решение:

(10)Ex(x,y)= F1(y+i*x)+ F2(y-i*x),

Здесь F1 и F2 – функции от одного аргумента, зависящие от граничных условий. Подчеркну здесь особо: следовательно, решение электростатического уравнения, как и всякого дифференциального уравнения в частных производных, зависит от граничных условий. Отсюда следует, что даже если известно распределение заряда в пространстве, это однозначно не определяет электрическое поле. Однако в учебниках и справочниках по физике явно игнорируется это обстоятельство. Готовые решения электростатических уравнений приводятся в них в привязке только к типу распределения заряда.

 

*** Классическое решение

Так, согласно [Яворский, Детлаф. Справочник по физике.] электрическое поле около заряженной прямой равно

Ex= rl/(2*Pi*e)*x/(x^2+ y^2), Ey= rl/(2*Pi*e)*y/(x^2+ y^2),

Где rl – погонная плотность заряда.

Но при каких граничных условиях? В некоторых источниках можно найти оговорку по этому вопросу: при условии, что Ex(infinity)=0, Ey(infinity)=0. C этим вроде бы можно согласиться, если и r(infinity, infinity)=0. Но, во-первых, с этим явно не согласуется, например, случай r= const не=0 (а кто нам запрещает рассматривать такое распределение заряда?). А во-вторых, а откуда следует, что граничные условия зависят от распределения заряда? Да нет же, в том-то все и дело, что это - вполне независимая величина, иначе не было бы смысла требовать отдельно задавать граничные условия. Да и к тому же уж слишком необычное граничное условие мы имеем в данном случае. Как его использовать для численного решения уравнения? И еще один серьезный вопрос: Ex и  Ey – это еще не все граничные условия для рассматриваемого уравнения. Так как оно 2-го порядка, то нужно задать еще dEx/dx(infinity) и dEx/dy(infinity). Про них же вообще нигде ни слова.

 

Есть и еще один пункт критики приведенного выше решения: оно удовлетворяет рассматриваемому нами уравнению нулевой правой частью, но такое поле (при неких граничных условиях, причем не обязательно связанных с бесконечностью) имеет место при dr/dx=0 и dr/dy=0. То есть при равномерно распределенном в пространстве заряде. Или, в отношении только одной из компонент поля при равномерном распределении вдоль одной оси координат. А не точечном, как утверждается в учебниках!

А как же сама плотность заряда? Неужели поле от нее не зависит? Зависит, только это связано с не с самими Ex и Ey, а как раз с их производными (см. уравнение (3)), то есть со 2-ой ветвью граничных условий.

 

** Симбиоз общего с классическим – как он достигается?

 

Но вернемся все-таки к рассматриваемому уравнению (9). Сначала несколько слов о его общем решении. Если, следуя требованию стремления E к 0 на бесконечности, в нем взять F1(x)= F2(x)= 1/x, то получается следующее решение:

E= 1/(y+i*x)+ 1/(y-i*x)= 2*y/(x^2+ y^2),

То есть то же самое, что выше (классическом решении) приведено для Ey. Если же взять F1(x)=1/(i*x), а F2(x)= -1/(i*x), то получится решение

E= 2*x/(x^2+ y^2),

То есть соответвующее приведенному выше для Ex. Но ведь это всего только два варианта даже для того граничного условия, которое иногда оговаривается в учебниках для решения электростатических уравнений. Например, этим же граничным условиям будет удовлетворять F1(x)= F2(x)= 1/x^2, почему бы не взять такой вариант?

Добавлю здесь еще одно соображение об общем решении (10): поскольку в него входят функции F1 и F2, аргументами которых являются в общем случае комплексные величины, то само собой очевидно, что не всякие варианты этих функций будут приводитьк физически осмысленным решениям. А значит, и не всякие граничные условия? Ведь с последними-то данные функции только и связаны.

 

** Один способ частного решения и что он дает

 

***

Наконец, рассмотрим один способ отыскания частных решений уравнения (7), отыскиваемых в условиях отсутствия граничных условий. Данный способ дает решения, заведомо имеющие физический смысл. Пусть ищется (какое-нибудь)решение уравнения

(9)d2Ex/dx^2+ d2Ex/dy^2= 0

Положим, что

(11)d2Ex/dx^2= C1, тогда (12)d2Ex/dy^2= -С1

Теперь, когда уравнение в частных производных превращено в два независимых обыкновенных дифуравнения, интегрируем эти уравнения по одиночке. Нюансом данного интегрирования является то обстоятельство, что Ex – это все-таки функция от 2-х переменных. Поэтому 1-ое интегрирование (11) дает

 dEx/dx= C1*x+ f1(y),

а 2-ое:

(13)Ex= C1/2*x^2+ f1(y)*x+ f2(y)

Теперь интегрируем (12):

 dEx/dy= -C1*y+ f3(x)

(14)Ex= -C1/2*y^2+ f3(x)*y+ f4(x)

Теперь остается совместить полученные два результата (13) и (14):

C1/2*x^2+ f1(y)*x+ f2(y)= -C1/2*y^2+ f3(x)*y+ f4(x)

Это получается при условии:

 f4(x)= C1/2*x^2, f1(y)*x= f3(x)*y, f2(y)= -C1/2*y^2

Что касается f4 и f2, то с ними все ясно. Разберемся теперь с f1 и f3. Уравнение для них (среднее) приводится к виду:

 f1(y)/y= f3(x)/x

Откуда немедленно следует, что обе части этого уравнения не зависят ни от x, ни от y, поскольку только так могут быть равны друг другу функции, зависящие от разных переменных. То есть, стало быть:

 f1(y)/y= f3(x)/x= K, откуда f1(y)= K*y и f3(x)= K*x

Общий итог таков:

Ex= C1/2*x^2+ K*x*y- C1/2*y^2

Не правда ли, на что-то похоже? Да это же наша знакомая гиперболическая поверхность!

 

***

Решим теперь тоже самое уравнение, но теперь положим

d2Ex/dx^2= C1*x => d2Ex/dy^2= -C1*x

в результате интегрирования получаем

dEx/dx= C1/2*x^2+ f1(y)

Ex= C1/6*x^3+ f1(y)*x+ f2(y)

dEx/dy= -C1*x*y+ f3(x)

Ex= -C1/2*x*y^2+ f3(x)*y+ f4(x)

Условия совмещения:

f4(x)= C1/6*x^3, f1(y)*x= -C1/2*x*y^2+ f3(x)*y, f2(y)=0

Из 2-го условия

f1(y)*x+ C1/2*x*y^2= f3(x)*y

x*(f1(y)+ C1/2*y^2)= f3(x)*y

Откуда

f3(x)/x= (f1(y)+ C1/2*y^2)/y= K

и далее

f3(x)= K*x, f1(y)= K*y- C1/2*y^2

Общий итог:

Ex= C1/6*x^3+ (K*y- C1/2*y^2)*x= C1/6*x^3+ K*x*y- C1/2*x*y^2

И опять наша старая знакомая – гипербола, а точнее – сумма двух гипербол, 3-его и 2-го порядков. Тогда как выше получалась сумма 2-х (разных)гипербол 2-го порядка. А между тем решалось ведь то же самое уравнение. Единственное различие – граничные условия. В 1-ом случае это были: Ex(0,y)= - C1/2*y^2, Ex(x,0)= C1/2*x^2. Поскольку в данном случае dEx/dx= C1*x+ K*y, dEx/dy= K*x- C1*y, то соответствующие граничные условия: dEx/dx(0,y)= K*y, dEx/dy(x,0)= K*x.

Тогда как во 2-ом случае Ex(0,y)= 0, Ex(x,0)= C1/6*x^3. Так как в данном случае dEx/dx= C1/2*x^2+ K*y- C1/2*y^2, dEx/dy= K*x- C1*x*y, то граничные условия: dEx/dx(0,y)= K*y- C1/2*y^2, dEx/dy(x,0)= K*x

 

***

Рассмотрим теперь 3-ий случай: d2Ex/dx^2= C1*y => d2Ex/dy^2= -C1*y

Интегрирование дает:

dEx/dx= C1*y*x+ f1(y), Ex= C1/2*y*x^2+ f1(y)*x+ f2(y),

dEx/dy= -C1/2*y^2+ f3(x), Ex= -C1/6*y^3+ f3(x)*y+ f4(x)

Условия совмещения:

C1/2*y*x^2+ f1(y)*x = f3(x)*y, f2(y)= -C1/6*y^3, f4(x)= 0

Из 1-го условия:

C1/2*y*x^2- f3(x)*y= -f1(y)*x

Откуда

y*(C1/2*x^2- f3(x))= -f1(y)*x =>

(-C1/2*x^2+ f3(x))/x= f1(y)/y= K =>

f1(y)= K*y, -C1/2*x^2+ f3(x)= K*x => f3(x)= K*x+ C1/2*x^2

Итоговое решение:

Ex= -C1/6*y^3+ (K*x+ C1/2*x^2)*y= -C1/6*y^3+ K*x*y+ C1/2*x^2*y

Найдем сразу dEx/dx= K*y+ C1*x*y, dEx/dy= -C1/2*y^2+ K*x+ C1/2*x^2. Итак, как и ожидалось, опять старая знакомая – гипербола, Но только граничные условия другие: Ex(0,y)= -C1/6*y^3, Ex(x,0)= 0, dEx/dx(0,y)= K*y, dEx/dy(x,0)= K*x+ C1/2*x^2.

 

*** Заключение

Можно было бы и дальше продолжать эти эксперименты, варьируя как правую часть уравнения (7)(распределение заряда), так и функцию разделения (чему полагается равной одна из производных), но я со всей ответственностью заявляю, что покуда эти вариации не выходят в область отрицательных степеней x и y, результатом решения разбираемого уравнения являются гиперболические поверхности – эти гармонические колебания в полярной системе координат.