©
Копылов Михаил
Предмет теории
вероятностей
Обычно считается, что
основным понятием в теории вероятности является вероятность (некая
математическая сущность). Но редко при этом кто задает себе вопрос: а
вероятность чего? И еще реже на него отвечают: вероятность события.
Не знаем ли мы
какие-нибудь аналогичные явления в науках? Возьмем, например, геометрию. Что
она изучает? Длины, углы, площади и т.п. Но длины, углы, площади чего? Фигур –
геометрических квазипредметов. Почему квази? Да потому, что фигурой является,
например, комната. Или кастрюля. Но фигура – это как бы часть их предметности.
То есть предмет, в котором содержатся не все их свойства. Нет, например, их
температуры, массы, химического состава материала, и.т.п. А оставлены только
пространственные свойства.
Итак, получается, что теория вероятности (несмотря на традиционное включение её в курс математики) (подобно геометрии) – это предметная теория. Поскольку она изучает специфическое свойство (вероятность) специфических предметов (событий).
Структура события
Но что это за штука
такая, событие? Каким, может быть, более известным вещам, оно соответствует?
Как оно устроено?
Возьмем пример (события) из учебника: из шляпы (наугад) вытащили шар. И он оказался белым. Итак, данное событие выражается в форме утвердительного высказывания (будем в дальнейшем называть их тезисами): шар (из некоторого конкретного множества. Но неизвестно, какой именно.) белый. Следовательно, структура (элементарного. То есть все остальные события суть комбинации таковых) события такова: свойство (в данном случае цвет) = значение (в данном случае - белый). А еще проще: X=A, где X – переменная, а A – константа. (Причем в данном случае константа - логического типа (белый-черный), но может быть и иных типов.)
В дальнейшем (в (сугубо) математической теории вероятности, где и понятие «событие» уже перестает фигурировать) переменную X начинают называть «случайная величина». При этом совершенно упуская из виду, почему она случайная. Да потому, что информация о том, о цвете какого именно шара говорится в данном тезисе (то есть аргумент этого тезиса) намеренно не принимается во внимание. Именно это и придает тезису (и переменной) случайный характер.
Вероятность
Определение вероятности события очевидно вытекает из специфики тех тезисов, у которых наблюдается свойство вероятности. А именно, пусть рассматривается вероятность события вида: цвет(x)=»цвет», где x (предмет события.
Еще также может быть процесс события.
(Это следует из определения события как фрагмента предметного мира. Которому соответствует тезис. См. ЯЗЫК КАК СИСТЕМА ОБОЗНАЧЕНИЯ)
Но эту тему пока развивать не буду.)
"пробегает" множество значений X
(например, все шары в данной шляпе. Или все жители города N (имеется в виду цвет волос данного жителя).
Множество Х мы в дальнейшем и будем называть универсумом данного события. Иногда его путают со множеством значений свойства события (или переменной события. Что то же самое). Но это не одно и то же.)
Тогда конкретное значение «цвет» (например, белый) выделит из множества X подмножество Хб. Отношение мощности множества Xб к мощности множества X и есть вероятность события «цвет(x)=белый»:
p(A)=M(Xб)/(M(X)
Приведу пример из жизни.
Допустим, к экзамену по сопромату студент подготовил (идеально) 20 вопросов, а
всего в экзамене 50 вопросов. Спрашивается, какова вероятность того, что
экзамен студент сдаст на «5»? Ответ: 20/50. А 30/50 – это вероятность получения
оценки «2». Стало быть, все остальные исходы – события невероятные.
Сложные события
Понимание того, что событию соответствует тезис
(а точнее – что оно (полностью) представляемо им. Как например, количество «пять» числом «5». То есть формально представляемо. Это означает, что все операции с событиями можно теперь делать на бумаге – путем операций с их формальными представлениями.), легко помогает понять и то, как можно строить сложные (комбинированные) события – за счет логических связок. Среди которых основные – и, или, не.
(Вот почему логика высказываний – это аналогичная теории вероятностей дисциплина, с той лишь разницей, что она исследует еще одно свойство (функцию) сложных тезисов (=утвердительных высказываний) – их истинность. А также те операции, которыми можно получать из тезисов им равносильные.)
Более того, решение многих задач по теории вероятностей представляет из себя построение искомого события из элементарных и определение его вероятности.
Вероятность и-события
Будем называть события вида {A and B} и-событиями, а вида {A or B} – или-событиями.
Из учебника [например: Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.] известна формула вероятности или-события:
P(A или B)= p(A)+p(B)-p(A и B)
Но допустим, что вы сомневаетесь, правильно ли вы её вспомнили. (Ну, например, вы думаете: а зачем здесь 3-ье слагаемое? Может, оно лишнее?) Как проверить это?
Очевидно, что некоторое число P имеет смысл как вероятность только при выполнении условия 0>P>1 (это следует из определения вероятности). Следовательно, из самой формулы сложной вероятности (в данном случае – или-события) должно получиться, что p<1 (если p1<1, p2<1. А также при p1,2>=0). Проверим это (введя для упрощения обозначения: p(A)=p1, p(B)=p2):
P(A или B)= p(A)+p(B)-p(A и B)=> p=p1+p2-p1*p2=
p1*(1-p2)+p2=>
ð
1-p=
1-(p1*(1-p2)+p2)= (1 –p2)+p1*(1-p2)= (1-p2)*(1-p1)=
(<1)*(<1)=(<1)=>
ð p=(<1),
(где (<1) обозначает неотрицательное число, меньшее 1)
Что и требовалось доказать.
Однако необходимо понимать, что данное доказательство – не является доказательством истинности вышеприведенной формулы. Оно есть лишь неудавшаяся попытка доказательства её ложности. Вот если бы нам удалось доказать, что при данных интервалах значений p1 и p2 значение не находится в этом же интервале (так было бы, например, для формулы P(A или B)= p(A)+p(B)), то это было бы и доказательством её ложности.
Как же доказать непосредственно вышеприведенную формулу? То есть доказать именно её истинность? Воспользуемся для этого формулой, известной из алгебры высказываний:
Not(A and B)= notA or notB
Из неё следует:
p(not(A and
B))= 1-p(A)*p(B) (так как p(A and B)=p(A)*p(B), а p(not(A))=1-p(A))
Пусть:
P(notA or
notB)= f(1-p(A), 1-p(B))
Попробуем в качестве f приведенную выше формулу (для вероятности или-события):
P(notA or notB)= (1-p(A))+(1-p(B))-(1-p(A))*(1-p(B))=
=
1-p(A)*p(B)
Следовательно, функция f найдена верно.
Вывод: P(A
or B)= p(A)+p(B)-p(A and B) – истинно.
Вероятность моста событий
Сложные события, как известно, изображаются в виде схем. А именно: и-событие – в виде последовательных событий (рис.1,а), а или-событие – в виде параллельного соединения событий (рис.1,б). Но из электротехники известно, что 2х-полярные элементы могут соединяться (в 2х-полярную схему) и в виде моста, (и что этот тип соединения – не сводим ни к последовательному ни к параллельному).
В связи с этим возникает вопрос: а что если вычислить вероятность моста событий (рис.1,в)?
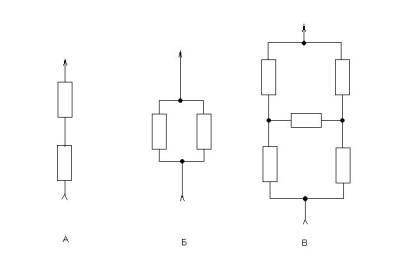
Рис.1. Простейшие сети событий.
Или такого не бывает в природе? То есть (такое соединение) не имеет физического (а точнее - предметного) смысла?
Ведь кроме «и» и «или» в логике нет других связок (не сводимых к ним). Есть, правда, еще «не». Но это – унарная связка. Хотя она и нужна для вывода других (из «и» и «или»))
Действительно, отсюда следует, что в любой схеме, интерпретируемой как сеть событий, (смежные) элементы должны быть соединены (=соотноситься) либо как последовательные, либо как паралелльные. В мосте же ни одной такой пары (элементов) нет. Поэтому мост не интерпретируем как сеть событий.
Совместность и зависимость
Базовыми понятиями теории вероятности являются несовместность и независимость событий (и, соответственно, контрадикторные им). Но нередко они путаются (особенно 2-ая пара). Хотя (как видно из предыдущего) различение и определение этих отношений между событиями весьма важно для вычисления вероятности сложных событий. Разберемся поэтому в этом вопросе более детально.
Несовместные события (согласно определению – см. Гмурман (выше)) – это такие, что
P(A or B)= p(A)+p(B)
То есть несовместные события – это непересекающиеся (рис.2,а):
p(A and
B)=0
(см. формулу для вероятности или-события в общем случае)
Независимые же события – это такие, что:
P(A and
B)=p(A)*p(B) (***)
Иначе: события A и B независимы (а точнее – событие B независимо от события A), если p(B/A)=p(B) (см. формулу для зависимых событий: P(A and B)=p(A)*p(B/A))
Внимание! Независимые события не следует путать с непересекающимися событиями. Почему возникает эта путаница? Потому что независимость событий – это частный случай несовместности событий – выход события в другое измерение.
(Вот уж где n-мерность, так да! Здесь n не ограничено значением 3, и причем интерпретируемо не ограничено)
Иначе говоря, в случае независимости события A и B - это события (в отношении) разных переменных. Например: A= {X=a}, B={Y=b} (рис.2,г) В логике это называется несравнимостью [Гетманова А.Д. Логика.] (Правда, это несравнимость вводится как отношение между понятиями. Однако выше мы увидели, что событие – это ни что иное, как признак (то есть некоторое содержание), а стало быть, отображается, как и понятие (а точнее – их объемы) в виде диаграмм Вьенна.)
Пересекающиеся же события – это всегда события одного измерения (А точнее – одного подмножества измерений. Например, когда сравниваются 2х-мерные события. В 3х-мерном универсуме (событий).)
Несовместные события смогут быть событиями как одного (рис.2,а), так и разных измерений (рис.2,г). Если они – разных измерений (=ортов), то они – независимы.
Таким образом события делятся сначала на совместные и несовместные, затем события несовместные делятся на одного измерения и разных измерений (так как совместные – это всегда одного измерения). А вот несовместные разных измерений – это все независимые.
Тогда получается, что зависимые события – это совместные (а значит – пересекающиеся) события?
Но ведь совместность – это не только классическое пересечение (событий) (рис.2,б) Есть и другой пример совместности – подчинение событий (рис.2,в).
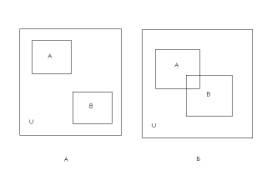
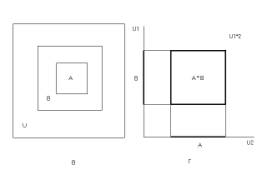
Рис.2. Виды отношений между событиями: а – несовместные, б – совместные, в – подчиненные, г – несравнимые.
При этом получаем:
p(B)=k*p(A),
где 0<k<1. Следовательно, k можно интерпретировать как некую вероятность (события B относительно события A):
p(B/A)=p(B)/p(A) (*)
то есть получили формулу, аналогичную формуле для зависимых событий. Как будто бы этот случай совместности есть зависимость событий.
Верно ли, что в данном случае p(B)=p(A and B) (как вроде бы следует из рис.)?
Ведь отсюда, учитывая (*), получим
P(A and B)= p(A)*p(B/A)
Как же так? Ведь выше была приведена формула для независимых событий: P(A and B)=p(A)*p(B)
А, понятно: P(A and B)= p(A)*p(B/A) - так для всех событий (-> случайных величин (СВ)).
А вот p(B/A)=p(B) – для независимых.
Но почему p(B/A)=p(B)? Ведь разве не p(B/A)=p(B)/p(A)? Откуда получается, что p(B/A)=p(B) имеет место не в любом случае, а при условии: p(A)=1.
Здесь явная путаница! Потому что в случае зависимых событий определение условной вероятности иное:
p(B/A)=P(A
and B)/p(A) (**)
А вот p(A and B)=p(B) (и p(B)=p(A)*p(B/A)) получается в том случае, если событие B подчинено событию A (что может быть только в случае их совместности). (Именно через эту подчиненность (событий) и определяется само понятие вероятности.)
Но ведь формула (**) подсказывает и еще одно определение:
p(A/B)=P(A
and B)/p(B)
Отсюда вывод: зависимость событий (в теории вероятности) не является симметричным отношением, как это имеет место в логике высказываний. Точнее говоря, мера этой зависимости может быть разной в ту (p(B/A)) или другую (p(A/B)) сторону. А в частных случаях (при подчиненности) - допускает и единичное значение в одну сторону при неединичном в другую.
Если же события непересекающиеся (=несовместные), то их зависимость (как в ту, так и в другую сторону. В виде условной вероятности) равна 0.
Таким образом, среди сравнимых событий тоже существуют
независимые?
Нет, это неверно. Потому что не соответствует формуле (***).
Поскольку для сравнимых несовместных событий
P(A and B)=0 (и не равно (тождественно) p(A)*p(B))
Вывод: независимые события в теории вероятностей – это то, что в логике называется несравнимые понятия (содержания). А зависимые – это сравнимые. Поскольку только для них можно вычислить условную вероятность p(A/B). Хотя бы она и равна 0.
Интерпретация зависимости событий
Как же тогда интерпретировать условную вероятность - p(B/A)? Ведь получается, что зависимость событий выражается в том, что вероятность зависимого события является долей вероятности события-аргумента: p(B)= p(B/A)*p(A), где p(B/A)<1.
С другой стороны, каким образом одно событие (A={x=a}) может влиять на другое событие (B={y=b})? Только при наличии функции: y(x). Но только понимаемой вероятностно.
Стало быть, зависимость событий – это, по большому счету, отражение случайной функции (причем случайной величины)= СлФСлВ, то есть связи между 2-мя случайными величинами. При этом связь y(x) уже выглядит (графически) не как линия, а как некий (размытый -> нечеткий) шнур в пространстве y0x.
То есть наличие события A еще не дает автоматически события B, но увеличивает его вероятность по сравнению с 0.
Отсюда следует, что о зависимости событий можно говорить и в отношении несравнимых событий. Если эти события таковы, что изменение вероятности одного из них (в зависимости от его расположения на шкале универсума) зависит от вероятности другого, то такие события
(а если быть совсем точным – полные
(или не обязательно? Да, не обязательно. Лишь бы бы их универсумы (а точнее – (теперь) под'универсумы) брались так, чтобы зависимость была заметна)
системы событий)
зависимы.
И совсем необязательно для определимости условной вероятности иметь общность универсума. Нет никаких проблем для вычисления условной вероятности для несравнимых. Так как для них вероятности вычислятся по разным универсумам:
P(A)=M(A)/M(Ua);
p(B)=M(B)/M(Ub)
Откуда, стало быть:
P(B/A)=
M(B)/M(Ub)/(M(A)/M(Ua))=M(A)/M(B)*M(Ua)/M(Ub)
В этом и
состоит путаница. А причина её – то, что в
теории вероятности до сих пор не
различаются сравнимость и несравнимость
понятий.
Эта необычная функция плотности распределения
Ввиду того, что переменная события (см. x, y) может иметь недискретный тип, в теории вероятностей вводится понятие функции плотности распределения f(x). Это такая функция, что вероятность события A вида x=(a1<a<a2) вычислится как:
P(A)=int(f(x),x=a1..a2)
Исходя из этого понятно, что данная функция – необычная. Интеграл её от –infinity до infinity обязательно конечен. Это эквивалентно (фактически) конечности интервала распределения (или размытости границ этого интервала. Иначе: интервал распределения (множество значений случайной величины) конечный, но границы его нечетки, вплоть до того, что простираются до бесконечности)
Это обстоятельство соответствует также как бы ограниченности (площади) универсума событий (который, повторюсь, (в общем случае) бесконечен). Поскольку иначе, согласно определению вероятности, её невозможно вычислить. Точнее, она для любого события получалась бы нулевой.
Существует ли природа этой ограниченности (универсума), а также природа (интегральной) конечности функций плотности распределения? Почему функцией плотности вероятности не может быть какая угодно функция? (Почему за бесконечность интервала универсума мы «расплачиваемся» специфическим видом функции плотности распределения?) И почему в природе господствует (вроде бы) нормальное распределение? Или хотя бы что-то (качественно) подобное (а математически – (как правило) производное от него) ему?
Вероятность
«0-ой толщины»
В основе определения вероятности лежит понятие о подчиненных событиях. (Чуть не сказал, что понятие об условной вероятности. Но это не так.)
То есть событие, вероятность которого определяется, должно лежать в том же универсуме (точнее, быть совместным с универсумом)
При этом оно должно быть той же размерности, что и универсум. Например, какова вероятность события, отображаемого прямой (как множества, представляющего событие) на плоскости (универсума)? Она равна 0. Потому что у прямой нет толщины. Следовательно, одномерное событие в 2х-мерном универсуме как бы не имеет смысла (не является событием).
Это свидетельствует о том, что 0 (как и infinity), по сути, в теории вероятности нет.
Однако это не соответствует истине. Ведь прямая, несмотря на свою 0-ую площадь, все же является множеством точек и имеет, стало быть, ненулевую мощность. Следовательно, вероятность события типа «прямая» в 2х-мерном универсуме отлична от 0. Как разрешить этот парадокс?
26.10-28.10.04
Впервые опубликовано 17.01.05
Изменения внесены 1.02.05