Преобразования систем координат и
преобразования фигур
©
Михаил Копылов
Школьные»
преобразования координат: смещение и сжатие (x1=x+a, x1= k*x).Факторы
преобразования СК и трансформации. Обратная зависимость между этими факторами.
Преобразование деформации как изменение единицы измерения.
В школьном курсе
математики есть такая тема: преобразование графиков. Это делается за счет
введения новых переменных и установления связи их со старыми. Пусть, например, x1=x+a. Пусть a>0. Тогда в новой СК график всякой функции
окажется смещенным вдоль оси X на a единиц влево. Сама же СК будет смещенной
(относительно старой СК) вправо. Назовем это преобразование смещением.
Другое преобразование, изучаемое в школе – это x1=k*x. Пусть |k|>1, тогда ось x новой СК оказывается сжатой относительно
старой в k раз. Это можно
проинтерпретировать как уменьшение единицы измерения (вдоль оси Х) в k раз. Но мы этого не замечаем, и поэтому
видим (в новой СК) все предметы растянутыми в k раз. Поэтому данное преобразование называют
сжатие-растяжение (или, для краткости, сжатие – с формальной
точки зрения сжатие и растяжение суть одно и то же, так как описываются одним
законом).
Но есть, как и в
предыдущем случае, и другая интерпретация тому, что мы видим при сжатии – сам
рассматриваемый предмет увеличился в размерах вдоль оси Х в k раз. Введем понятие фактора
преобразования (и трансформации): для смещения это будет величина a, а для сжатия – величина k. Различим также преобразования СК и
преобразования самих объектов, рассматриваемых в этих СК. Назовем последние трансформациями,
чтобы отличить от первых. Так вот, на материале уже 2-х преобразований мы видим
следующую закономерность: фактор трансформации противоположен фактору
соответствующего ему преобразования. То есть СК смещается вправо, а сам объект
– влево, СК сжимается в k раз,
а сам объект – в k раз
растягивается.
Центр
сжатия. Перемещения и деформации как виды трансформаций. Детерминант (степень)
деформации (постановка вопроса)(по сохранению расстояний, углов, телесных углов
и т.п.)(а также площадей, объемов и т.п.).
Понятие
аксессуара преобразования. Аксессуар смещения и сжатия – прямая.
Сравним две
вышеприведенных трансформации. Во-первых, бросается в глаза, что сжатие
отличается от смещения тем, что для него существует точка, которая при
трансформации переходит сама в себя. Её легко найти из уравнения x1=k*x=x,
откуда искомая точка x=0.
Назовем её центром сжатия. Но пусть, например, сжатие описывается
законом x1=b+k*x. Тогда центр сжатия найдется из b+k*x=x
=> x=-b/(k-1)
(а не x=b, как первоначально кажется)
Другое отличие
сжатия от смещения – это то, что оно изменяет расстояния. Поскольку в 1-мерном
пространстве расстояние характеризует величина dx, то для сжатия x1=k*x получаем: d(x1)=
d(k*x)=
k*dx. Следовательно, эта трансформация
увеличивает (все) расстояния в k раз.
Назовем все трансформации, изменяющие расстояния, деформациями, а
не изменяющие – перемещениями. Правда, при этом остается вопрос:
а что если трансформация не изменяет расстояния, но изменяет углы (или площади,
или объемы)? Следует ли при этом её считать деформацией? Разумеется, следует. И
по большому счёту нужно перемещения определить как трансформации, не изменяющие
никаких геометрических функций объекта. Однако при это мы получим
(логически) неполное определение, поскольку понятие геометрические функции
объекта никак не ограничено. Например, в вышеприведенном списке геометрических
функций отсутствует телесный угол, а почему бы не быть еще какой-нибудь
разновидности угла? К тому же пока у нас нет инструмента (детерминанта),
который бы по закону трансформации определял изменение конкретной
геометрической функции, за исключением расстояния. В связи с этим отложим этот
вопрос на будущее и ограничимся пока данным выше определением перемещений.
Теперь о сходстве
смещения и сжатия. Для рассматриваемых трансформаций очевидно, что обе они
происходят вдоль оси Х. Но ось Х, как геометрический элемент, - этот прямая.
Значит, для осуществления этих трансформаций необходимо задание некоторой
прямой. Это, конечно, не совсем очевидно для 1-мерного пространства, в котором
существует всего одна прямая. Но при переходе к 2-м измерениям это становится
вполне очевидно. Введем теперь понятие аксессуара трансформации
как геометрического элемента, необходимого для задания трансформации.
Следовательно, мы можем сделать вывод: аксессуар смещения и сжатия – это
прямая.
Переход
в 2х-мерную СК. 2х-мерный закон смещения. Аксессуар смещения – прямая. Способ
отыскания аксессуара типа прямая.
Перейдем в 2х-мерное
пространство. В нем закон рассмотренного выше смещения выглядит как {x1=x+a, y1=y}. Но поскольку аксессуар смещения – это
прямая, то имеет смысл говорить о смещении вдоль произвольной прямой. Как
выглядит закон такого смещения? Исходя из вида закона смещения для 1-мерного
случая можно предложить только следующий: x1=x+a, y1=y+b.
Пусть, например, a=b=1, тогда смещение приводит к следующему
результату (рис.1).
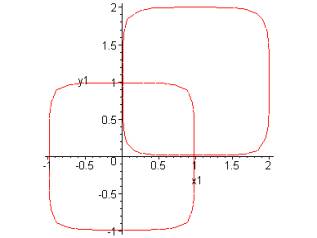
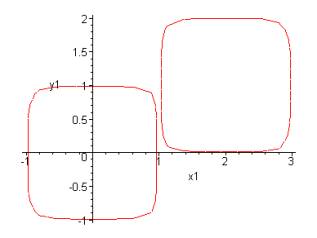
Рис.1. Смещение по
закону x1=x+1, y1=y+1 Рис.2. Смещение по закону x1=x+2,
y1=y+1
То есть происходит смещение
вдоль прямой y=x. Зададим теперь иной закон смещения и
посмотрим на результат (рис.2) Видно, что данное смещение происходит вдоль
прямой, соединяющей старый и новый центры объекта – точку (0,0) и точку (2,1).
Эти условиям удовлетворяет прямая y=x/2. Но как отыскать её аналитически? Ответ
подсказывает следующее наблюдение: данная прямая в результате смещения
переходит сама в себя. Пусть В результате исследуемого смещения искомая прямая
переходит в прямую x1/A+y1/B=f.
Следовательно, до смещения её уравнение было (x1-2)/A+(y1-1)/B=f.
Поскольку требуется идентичность этих прямых, то x1/A+y1/B=(x1-2)/A+(y1-1)/B, откуда –2/A-1/B=0
и A=-2*B. Следовательно, уравнение искомой прямой -x1/(2*B)+y1/B=f,
Таким образом, получили семейство прямых x1/2-y1=f*B=f1, где f1 – произвольная константа. Значит, то, что
мы получили выше (y1=x1/2)– это было частным случаем.
В общем же случае,
то есть аксессуаром смещения с законом x1=x+a, y1=y+b
является прямая (точнее, семейство прямых) x/a-y/b=f.
2х-мерный
закон сжатия. Аксессуар сжатия – не прямая (после применения способа отыскания
прямой) Аксессуар сжатия – точка (центр сжатия)
Закон сжатия,
рассмотренный выше, в 2х-мерном пространстве выглядит так: x1=k*x, y1=y. Поскольку выше был сделан вывод, что
аксессуаром сжатия тоже является прямая, то имеет смысл говорить также, как и в
случае смещения, о сжатии вдоль произвольной прямой. Каково уравнение такого
сжатия? Для этого посмотрим на 2х-мерное распространение закона сжатия (x1=k*x, y1=m*y)
и применим этот закон на практике (рис.3, 4)

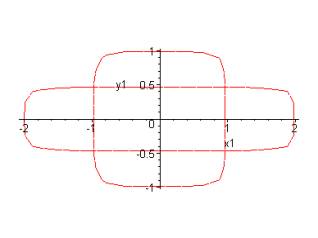
Рис.3. k=2, m=3/2 Рис.4. k=2, m=1/2
Как видно из рис.3 и
рис.4, деформация объекта происходит не только воль осей Х и У, но и во всех
направлениях, и причем в каждом по-разному. Более того, в 2х-мерном
пространстве появляется возможность сочетать в одной трансформации как
растяжение, так и сжатие (рис.4). Общей формулы степени деформации (по
расстоянию) не существует, но можно узнать эту величину вдоль конкретной
прямой. Пусть это прямая y=x, тогда dy= dx
и r1^2= (dx1)^2+ (dy1)^2=
k^2*(dx)^2+ m^2*(dy)^2= (k^2+m^2)*(dx)^2. Понятно, что если направление (точнее,
прямую) деформации взять иную, то и степень деформации получится другая.
Всё это наводит на
мысль, что аксессуар сжатия – всё-таки не прямая, а нечто иное. Но попробуем
вычислить эту прямую тем методом, который использован выше для смещения. Пусть
после преобразования искомая прямая имеет вид A*x1+B*y1=f, тогда до преобразования она имела вид A*x1/k+B*y1/m=f. Исходя из требования идентичности этих
прямых получаем уравнение A*x1+B*y1= A*x1/k+B*y1/m. Отсюда имеем систему {A=A/k, B=
B/m}. Если k<>0 и m<>0, то решение этой системы {A=0, B=0}.
В итоге получается, что искомая «прямая» 0*x1+0*y1=f. При f=0 полученная связь является тождеством (то
есть ему удовлетворяет любая точка плоскости), в противном же случае –
антитождеством (то есть ни одна точка плоскости ему не удовлетворяет). Этот
результат может быть понят только как отсутствие у трансформации сжатия
аксессуара типа прямая. Что же тогда (какого же типа аксессуар) имеет сжатие?
Вспомним, что выше,
для 1-мерного сжатия мы вычисляли его центр. Попробуем это сделать для
2х-мерного сжатия. Центр сжатия определится из системы: {k*x=x, m*y=y},
откуда, опять же при k<>0
и m<>0, получаем {x=0, y=0}
– это и есть центр (исследуемой) трансформации типа сжатие. Стало быть,
аксессуар сжатия – это точка.
Поворот как
исконно 2х-мерное перемещение. Аксессуар поворота – точка. Сохранение углов при
повороте. Элементарные повороты: 1)x1=-y, y1=x (на Pi/2 против часовой); 2)x1=y, y1=x (ложный поворот, осевая симметрия – поворот
в 3-ем измерении)
Следующее широко
известное преобразование – это поворот. Это преобразование изучается в высшей
школе. Его закон записывается довольно сложно: x1=x*cos(f)-y*sin(f),
y1= x*sin(f)+y*cos(f).
При повороте сохраняются расстояния, это легко доказать приведенным выше
методом вычисления dx1^2+dy1^2 и сравнения его с dx^2+dy^2.
Этим же способом доказывается, что более общее преобразование x1=x*A-y*B, y1=
x*B+y*A имеет степень деформации (изменения
расстояния) sqrt(A^2+B^2).
Итак, поворот – это перемещение, причем исконно 2х-мерное, поскольку в 1-мерном
мире его просто не может существовать (исходя из формы закона поворота).
Очевидно, и мы не будем углубляться в доказательство того, что аксессуаром
поворота также (как и для сжатия) является точка, вокруг которой и происходит
поворот – центр поворота.
Но не так очевидно,
что при повороте, как и при упомянутом выше более общем преобразовании {x1=x*A-y*B, y1=
x*B+y*A} сохраняются углы. Как доказать это? Пусть
конечная прямая имеет уравнение k*x1-y1=
b. Поскольку углы между
прямыми сохраняются при параллельном переносе прямых, то без ограничения
общности рассуждений можно положить b=0.
Тогда уравнение исходной прямой k*(x*A-y*B)-(x*B+y*A)=0
=> x*(k*A-B)-y*(k*B+A)=0 =>
x*(k*A-B)/(k*B+A)-y=0. Поскольку k=tg(a1),
а (k*A-B)/(k*B+A)=tg(a2) (где a1 и a2
– углы наклона соответствующих прямых к оси Х), то нужно найти tg(a2-a1)= (tg(a2)-tg(a1))/)(1+tg(a2)*tg(a1)).
Вычисления дают: tg(a2-a1=-B/A,
то есть не зависит от k –
параметра исходной прямой. Это и говорит о том, что данное преобразование {x1=x*A-y*B, y1=
x*B+y*A} сохраняет углы, поскольку любая прямая
поворачивается на один и тот же угол.
Пусть в обобщенном
преобразовании A=0, B=1, тогда получим закон {x1=-y,
y1=x} Несмотря на свою простоту, это – тоже закон
поворота, а именно на угол Pi/2
против часовой стрелки. Если поворачивать по часовой стрелке, то получится
преобразование {x1=y, y1=-x} Есть еще одно интересное преобразование, с
виду кажущееся сжатием (в отрицательное количество раз): x1=-x,
y1=-y. Но на самом же деле это – тоже поворот, на
угол Pi, как против, так и по
часовой стрелке (такой угол!)
Наконец, есть еще
преобразование, очень похожее на вышеприведенные по форме: x1=y,
y1=x, но не являющееся поворотом. Это – осевая
симметрия относительно оси y=x. Другая его интерпретация – это поворот, но
с выходом в 3-ье измерение – поворот (плоскости) вокруг указанной прямой на Pi, а не поворот внутри плоскости.
Сдвиг как
развитие поворота и исконно 2х-мерная деформация. Виды сдвигов (по y). Аксессуары сдвига: точка и … прямая. Сдвиг
– синтез поворота и смещения.
Поскольку сжатие не
представляют из себя исконно 2х-мерной деформации, поищем таковую. Таковой
является деформация сдвига, считающаяся одной из основных в физике[1].
Какой закон описывает деформацию сдвига?
Его легко получить из следующих соображений: пусть сдвиг происходит
вдоль оси Х, тогда ординаты всех точек остаются неизменными (то есть y1=y),
а абсциссы смещаются на величину, зависящую от y, в простейшем случае - пропорциональную y (то есть x1= x+ y*tg(fi),
где fi – угол сдвига, от вертикали – оси У) Таким
образом, вырисовывается следующий закон, описывающий сдвиг: x1=x+y*tg(fi), y1=y. Что из него следует? Что сдвиг происходит
вдоль некоторой прямой, в том смысле, что все точки при сдвиге перемещаются по ней
и параллельным ей прямым (семейству параллельных прямых, чему
естественно дать название «направление», в данном случае смещения) Значит, сдвиг имеет аксессуар типа
прямая. (Значит, можно себе помыслить сдвиг вдоль произвольной прямой.) Кроме этого, на перпендикулярной ей прямой
обязательно имеется точка, относительно которой задается закон смещения. В приведенном
выше случае это y=0.
Точнее говоря, это даже не точка, а прямая – как бы главная прямая семейства «направление»
Все точки на этой прямой характерны тем, что их смещения при сдвиге равны 0.
Все же прямые, перпендикулярные ей, при сдвиге поворачиваются на один и тот же
угол (fi) вокруг точек
пересечения с ней. Поэтому сдвиг предстает как некий синтез смещения и
поворота.
Рассмотренный сдвиг
сохраняет все расстояния вдоль прямых направления, а также вдоль перпендикулярных
ему прямых. Но вдоль всех других прямых расстояния не сохраняются – это легко
вывести из закона сдвига. Поэтому сдвиг является деформацией. Не сохраняет
сдвиг также и углы – в отличие от сжатия.
Но можно себе
помыслить и другой тип сдвига. Зафиксируем точку на оси У и повернем эту ось на
угол fi. И пусть все точки на
параллельных оси У прямых смещаются точно так же. Тогда будет изменяться и y, и получим закон {x1= x+ y*sin(fi), y1=y- y*cos(fi)= y*(1-cos(fi))} При таком сдвиге расстояния не сохраняются уже вдоль осей
направления и перпендикулярных им, но сохраняются вдоль прямых вида y= (x-a)*ctg(fi). Хотя это тоже (как бы) синтез смещения и
поворота, но уже иной.
Таким образом, в
общем случае сдвиг описывается законом {x1=x+A*y,
y1= B*y}
Хотя требования сохранения расстояний вдоль некоторых прямых, конечно же, накладывают
ограничения на A
и B – создают связь между ними. Так же, как требования отсутствия
деформаций создают связь между параметрами общего закона поворота (см. выше).
Эту связь, для сдвига, мы предоставляем отыскать заинтересованному читателю.
Сдвиг может быть
также интерпретирован как смещение, параметр которого зависит от другой
координаты.
Обобщение
закона 2х-мерных трансформаций. Разложение произвольной 2х-мерной трансформации
на элементарные.
Все же рассмотренные
выше трансформации, как нетрудно увидеть, описываются общим законом вида {x1= A*x+ B*y+ С, y1= D*x+ E*y+ F}.
Но если разобранные выше трансформации (смещение, сжатие, поворот и сдвиг) действительно
являются элементарными, то общий закон должен сводиться к комбинации этих
элементарных трансформаций.
Начнем со смещения.
Поскольку оно в 1-ую очередь выделяется из общего закона. А именно, если сначала
сделать трансформацию {x1= A*x+
B*y, y1=
D*x+ E*y}, а потом смещение {x2= x1+
C, y2= y1+
F}, то тогда и получим
вышеприведенный общий закон. Очевидно, что теперь дело сводится к декомпозиции
остатка {x1= A*x+
B*y, y1=
D*x+ E*y}. Очевидно также, что остаток не содержит
себе никакого смещения.
Что проще выделить
на 2-ом этапе? Это может быть либо поворот, либо сжатие, причем общего случая, то
есть эллиптическое. Скорее всего, начать следует со сжатия. Но параметры сжатия
нужно подобрать так, чтобы в остатке получилась комбинация только поворота и
сдвига. Пусть сжатие происходит по закону {x2= sqrt(A^2+B^2)*x1,
y2= -D/B*sqrt(A^2+B^2)*y1},
тогда в остатке получается трансформация {x1= (A*x+ B*y)/sqrt(A^2+B^2), y1= -B/D*(D*x+ E*y)/sqrt(A^2+B^2)= (-B*x-E*B/D*y)/sqrt(A^2+B^2)}. Нетрудно видеть, что если из неё
выделить сдвиг {x2=x1, y2=
y1- (E*B/D+ A)/sqrt(A^2+B^2)}, то останется чистый поворот {x1= (A*x+B*y)/sqrt(A^2+B^2), y1= (-B*x+A*y)/sqrt(A^2+
B^2)} Немного труднее
сначала выделить поворот, но так или иначе теорема доказана: указанные выше
трансформации являются элементарными. И сдвиг, как элементарное преобразование,
получается естественным образом - при первоначальном выделении поворота.
Обратите внимание:
при декомпозиции использовался сдвиг 1-го типа. Сдвиг же 2-го типа, {x1= x+
y*sin(fi),
y1= y*(1-cos(fi))} может быть, очевидно, тоже декомпозирован
– на эллиптическое сжатие и сдвиг 1-го типа. И, возможно, еще поворот. Предлагаем
рассмотреть этот вопрос читателям.