Сечение пирамиды плоскостью, параллельной медиане её боковой грани (№1)
Дано:
Основанием пирамиды ТАВС служит
равносторонний треугольник АВС со стороной равной
4√3. Высота пирамиды совпадает с боковым ребром ТА. В пирамиде проведена плоскость проходящая через вершину С, середину бокового ребра ТА (т.N) и параллельна медиане АМ боковой грани ТАВ.
Найти: площадь сечения, если расстояние от медианы до плоскости равно 2.
Решение
Основная трудность этой задачи – в построении. А именно – в построении плоскости, параллельной медиане боковой грани (АМ) и проходящей через прямую NC. А плоскость эта изобразится прямыми-пересечениями её с другими гранями пирамиды: TAB и TAC. Пересечение со 2-ой гранью очевидно – это прямая NC. Пересечение с гранью TAB найдется как прямая NK, параллельная AM (так как эта прямая лежит одновременно в плоскости, параллельной AM (по условию) и в плоскости TAB, которой также принадлежит прямая AM). В итоге получим сечение пирамиды искомой плоскостью – треугольник NCK (см. рис.1)
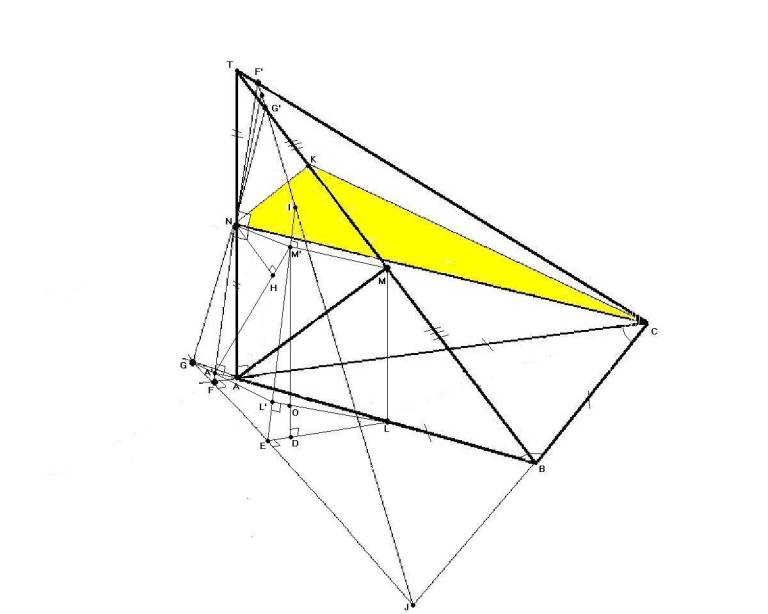
Рисунок 1.Вспомогательные построения
Поскольку в условиях дано расстояние от AM до NC, то нужно построить этот отрезок. Сначала проведем через точку N плоскость, перпендикулярную NC. Пусть прямая NF перпендикулярна NC (будем записывать это как n(NF,NC)) и лежит в плоскости TAC (=in(NF,TAC)), тогда она пересечет прямую AC в точке F (запишем как t(NF,AC)=F). Пусть NG: (=NG - такая, что) {p(NG,NC), in(NG,TAB)} (фигурные скобки означают логическую связку «и»), тогда t(NG,AB)=G. Отсюда плоскость n(NFG,NC) и in(GF,ABC). Поэтому t(GF,BC)=J.
Пусть также t(NG,TB)=G’, t(NF,TC)=F’, тогда F’G’=t(NFG,TBC). Поэтому t(F’G’,BC)=t(GF,BC)=J (ведь GF=t(NFG,ABC) по построению).
Докажем, что n(AF,FG). Так как из условия n(NA,ABC), то A=op(N,ABC) (A – ортогональная проекция N на плоскость ABC) => FA=op(FN,ABC). Так как n(NFG,NC), то n(FG,FA) (поскольку как прямые FA=AC). Тогда по теореме 3-х перпендикулярах n(FN,GF) и n(NAF,NGF).
Далее пусть {p(AA’,NC) in(A’,FN)} => n(AA’,FN). Поэтому
A’=op(A,NFG).
Построим теперь op(M,NFG). Для этого нужно
провести через точку M плоскость x:
p(x,NAD) (параллельную пл-ти NAD). Пусть
p(ML,NA) => in(ML,TAB) и in(ML,x) => ML=t(x,TAB). Так как in(L,AB), то LE: p(LE,AD) => in(LE,ABC) =>
t(LE,GF)=E и in(LE,x). Наконец, из p(EI,DN) => in(EI,x) и in(EI,NGF). Итак, x=MLE. Из in(EI,NGF) => t(EI,F’G’)=I.
Остается теперь провести MM’: n(MM’,EI) и in(M’,EI) (=> p(MM’,NC)). В итоге M’=op(M,NFG) => A’M’=op(AM,NFG). Пусть теперь n(NH,A’M’) и in(H,A’M’), тогда l(NH) (длина NH) – расстояние от NC до AM (=d(NC,AM)).
На этом (геометрическое) построение закончено.
Приступим теперь к построению мат.модели задачи. (Далее
идентификаторы отрезков применяются в значении их длины (=l(_)).)
Искомая площадь s(NKC)=f1(NK,KC,NC) (по формуле Герона) (1)
Понятно, что все параметры, связанные (исключительно) с пирамидой, определятся исходя из AB=BC=AC=a и TA=h. Поскольку 1-ая величина известна из условия, то 2-ая найдется из уравнения, связывающего её и AB c NH=d.
Из g(TNK,TAM) (=подобия треугольников TNK и TAM) и TN=NA =>
NA=TA/2, NK=AM/2
и TK=TM/2 (2a,b,c)
Очевидно, что из n(TAB)
(=прямоугольности треугольника TAB)
и TM=MB =>
TM=TB/2 и AM=f2(TA,AB) (3a,b)
Из n(TAC)
и TN=NA найдется NC=f3(TA,AC) (4)
KC? Из
TCB KC=f11(TA,BC,TK)
Найдем теперь связь TA и AB c NH=d (*).
Из NA’M’ NH=f7(NA’,A’M’,NM’) (5)
Из n(NAF)
и n(AA’,FN)
NA’=f8(FA,NA), AA’=f9(FA,NA) (6a,b)
Из треугольника FCF’ и n(FF’,NC) FF’=f4(TA,AC), FN=f5(TA,AC),
FA=f6(TA,AC) (7a,b,c)
Из трапеции AMM’A’ A’M’=f10(AA’,AM,MM’)
(8)
Чтобы найти MM’, в 4х-угольнике MM’EL проведем M’D: p(M’D,TA) и LL’: p(LL’,NC). В итоге получим n(M’DE) и n(LL’E).
MM’=OL, OL=L’L-L’O
(9)
Из g(LL’E,AA’F)
LL’/AA’=L’E/A’F=EL/FA => LL’= EL/FA*AA’ (10)
Из g(GEL,GFA)
EL/FA=LG/GA=GE/GF => EL=LG/GA*FA и g(L’EG,A’FG) (11)
LG=GA+AL,
AL=AB/2 (из TM=TB
и n(ML,AB))
(12)
Из n(AFG)
GA=FA/cos(pi/3)=2*FA (13)
L’O=? Из n(OL’M’) L’O=M’O/sin(OM’L’)
(14)
Из g(M’DE,NAF) c(OM’L’)=c(ANF) (равны угловые меры углов)
M’O=ML=TA/2
(15)
NM’=?
Из g(M’L’O,NA’A) M’L’/NA’=M’O/NA=1
=> NA’=M’L’
Из n(OL’M’)
M’L’= M’O/cos(OM’L’)
Из p(M’L’,NA’)
NM’=A’L’
A’L’=GL’-GA’
Из g(L’EG,A’FG)
GL’/GA’=GE/GF
GF? Из n(AFG) GF=FA*tg(pi/3)=sqrt(3)*FA
Учтя все связи, начиная с (5), получим искомое уравнение (*), решение которого даст значение TA. А подставив найденное значение в связи (1-4), найдем искомую s(NKC).