Равномерное и неравномерное прямолинейное движение
№95.
Книга находится:
А) в покое так как книга относительно стола не перемещается;
б) движется, так как перемещается вместе с поездом относительно рельсов;
в) в покое, так как книга относительно пола не перемещается;
г) движется, так как книга вместе с поездом перемещается относительно столбов.
№96.
Прямая линия.
№97.
Обе стрелки движутся по окружности. Минутная стрелка движется быстрее и окружность, которую она описывает, большего радиуса.
№98.
Окружность.
№99.
Прямолинейные траектории: рама, руль, сиденье, криволинейные — точки обода колеса, цепь.
№100.
Скорости станции и кораблей одинаковы, так как они не перемещались относительно друг друга, то их скорости относительно друг друга равны 0.
№101.
В полдень, когда направление движения поверхности Земли совпадает с направлением движения Земли вокруг Солнца.
№102.
Так как движутся самолеты с одинаковой скоростью, то их скорости относительно друг друга равны 0.
№103.
Вверх с такой же по модулю скоростью, т. е. со скоростью 5 см/с.
№104.
Одинаковые.
№105.
Одинаковые.
№106.
Проекции векторов перемещения на оси координат:
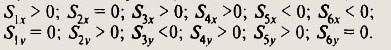
№107.
Сделаем пояснительный рисунок.
Определим расстояния между этажами

№108.

№109.
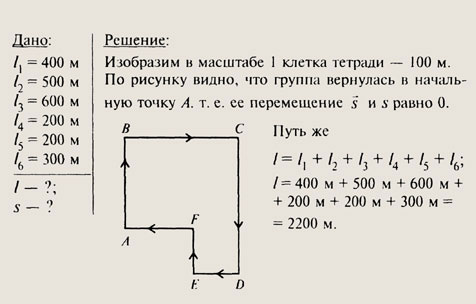
№110.

№111.
Наибольшей является скорость на участке СД наименьшей на участке ВС. так как расстояние CD наибольшее, а ВС наименьшее, а скорость — отношение расстояния проходимого телом за промежуток времени к этому промежутку.
№112.
Средняя скорость больше на участке вг, так как при одинаковом времени, расстояние SВг > SАб, a v = s/t. Следовательно
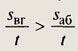
№113.
Нет такое движение назвать равномерным нельзя, так как движущая льдина могла перемещаться не все время, а например несколько часов, а все остальное время не двигалась.
№114.
![]()
№115.
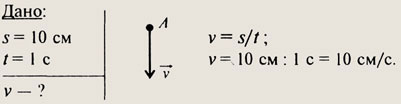
№116.

№117.

№118.
V = 36 км//ч = 36 • (1000 м/3600 с) = 10 м/с.
№119.
V| = 7,9 км/с = 7,9 • (1000 м/с) = 7900 м/с.
V|| = 11,2 км/с = 11,2 • (1000 м/с) = 11200 м/с.
V||| = 16,7 км/с = 16,7 • (1000 м/с) = 16700 м/с.
№120.

№121.

№122.

№123.

№124.
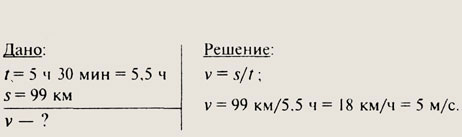
№125.

№126.

№127.

№128.

№129.

№130.

№131.

№132.

№133.

№134.
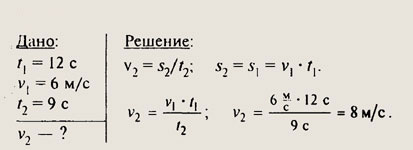
№135.

№136.

№137.

№138.

№139.

№140.

№141.

№142.
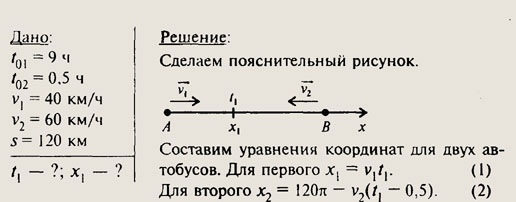
Второе тело находится в движении на 0,5 ч меньше первого, поэтому (t1 — 0,5) ч — это его время движения. Так как в месте встречи тела имеют одинаковые координаты и время встречи одинаковое, то, приравняв уравнения (1) и (2), найдем время движения автобусов до встречи и, подставив его в уравнение (1), найдем расстояние места встречи от точки А.
V1 • v2 = 120- v2(t1 — 0,5);
40t1 = 120-60 (t1 -0,5);
40t1 = 120 — 60t + 30;
100t1 = 150;
T1 = 1,5(4);
Х1 = 40 — 1,5 = 60 (км).
Автобусы встретятся 4ерез 1,5 ч после выхода первого автобуса в 60 км от точки А.
№143.

№147.
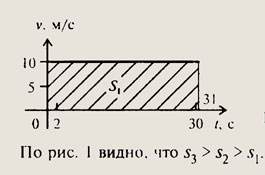
Равномерно движется только первое тело, так как график — прямая линия, а особенностью равномерного движения является то, что график, выражающий это движение, имеет вид прямой линии, так как зависимость между величинами скорости и пути прямо пропорциональна.
Тела 2 и 3 тоже могут двигаться не тольо прямолинейно, но при этом ускоренно или замедленно.
№148.
По графику выписываем данные и решаем задачу.

№149.
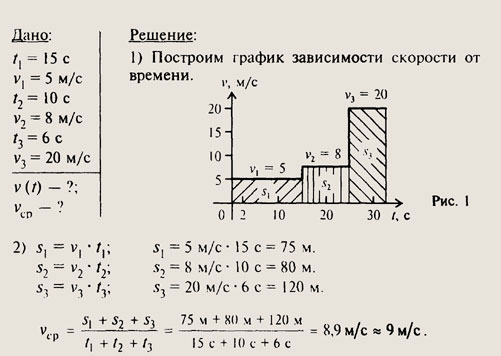
№150.
1. Скорости движения тел по графикам можно определить по формуле
![]()
— начальная координата тела, х — координата тела через время t.
Для тела 1: v1 = (1 — 1): 4 = 0, т. е. скорость тела равна 0.
Для тела 2: v2 — (3 м — 0 м): 5 с = 0,6 м/с.
Для тела 3: v3 = (6 м — 4 м) : 5 с = 0,4 м/с.
Для тела 4: v4 = (8 м — 6 м) : 5 с = 0,4 м/с.
Для тела 5: v5 = (8 м — 10 м): 5 с = -0,4 м/с, т. е. тело движется навстречу телам 1, 2, 3 и 4.
2. Точки пересечения графиков говорят, что тела либо встречается при движении либо одно тело догоняет другое. По данному рисунку видно, что 2-е тело догнало 1-е тело приблизительно через 1,5с после начала своего движения. 5-е тело встречалось с 4-м телом через 5 с после начала движения.
3.
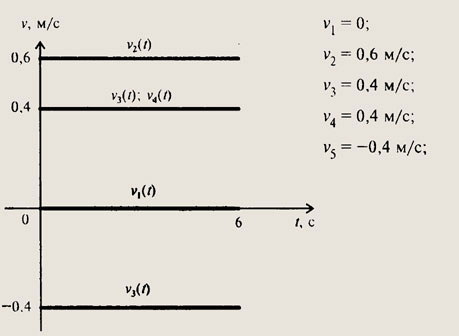
№151.
I. Уравнение зависимости координаты от времени имеет вид х = x0 + vX T (1). здесь x0 — начальная координата, т. е. положение тела в момент времени
![]()
— скорость тела.
На рисунке в учебнике графики движения 3-х тел. Для каждого из них надо определить x0 и vX и подставить их в формулу (1).

II. а) Для нахождения координат тел по графикам надо из точки t = 5 с восстановить перпендикуляр до пересечения с графиком и провести прямую перпендикулярную оси х. Итак, по графику через 5 секунд х1 = 5 м; х2 = 0 (м); x3 = -7,5 (м).
Б) Чтобы найти координату тела через некоторое время по уравнению координаты надо в уравнение координаты поставить соответствующее время:
Х1 =5 (м); x2 = 5 — 1 • 5 = 0 (м); х3 = -10 + 0,5 • 5 = -7,5 (м).
III. Время и место встречи определяем по точке пересечения графиков. Перпендикуляры, опущенные из точки пересечения графиков на оси времени и координаты дают нам время и место встречи (tA; ХA ): tA = 10 с; xA = -5 м.
Второе и третье тела встретились через 10с после начала движения в точке с координатой -5 м.
№152.

№153.
График скорости равномерного прямолинейного движения — прямая, параллельная оси времени, гак как скорость со временем не изменяется ни по величине ни по направлению. Итак, графиком равномерного прямолинейного движения является график 4. Точка пересечения графиков 3 и 5 указывает, что примерно через 1,2 с после начала движения 3-го и 5-го тел скорости этих тел стали одинаковыми, но утверждать, что координаты тел стали одинаковыми, нельзя.
№154.
I. Начальные скорости движения — точки пересечения графиков функций с осью v. Так v01 = 0 (м/с); v02 = 14 (м/с); v04 = 9 (м/с); v04 = 8 (м/с).
II. Приращение скорости за 1 с обозначим ▲v/▲t, здесь ▲v -изменение скорости за время ▲t.
![]()
Скорость со временем не изменяется.
III. Для определения средней скорости за 6 с надо путь, пройденный телом за 6 с, разделить на время 6 с. Путь можно найти как площадь фигуры, описанной графиком за 6 с.

№155.
№156.

№157.
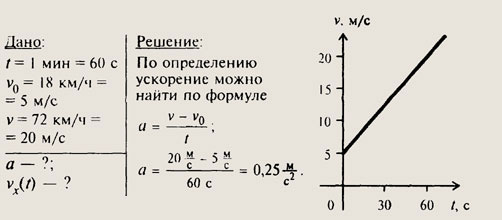
Зависимость скорости от времени имеет вид v = v0 + at, где v0 — начальная скорость движения тела, а — ускорение движения. Рассмотрим каждый график в отдельности.


№158.

№159.

№160.

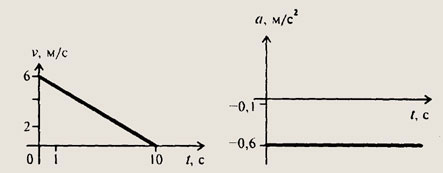
Рис к №160.
