§ 5. Геометрические построения → номер 47
Пусть даны два отрезка а и d и угол α.
Нужно построить ΔАВС, в котором ВС = а, ∠В = α, а |AC — AB| = d.
Задача имеет решения лишь при d < a, т. к. из неравенства треугольника следует, что любая сторона должна быть больше разности двух сторон.
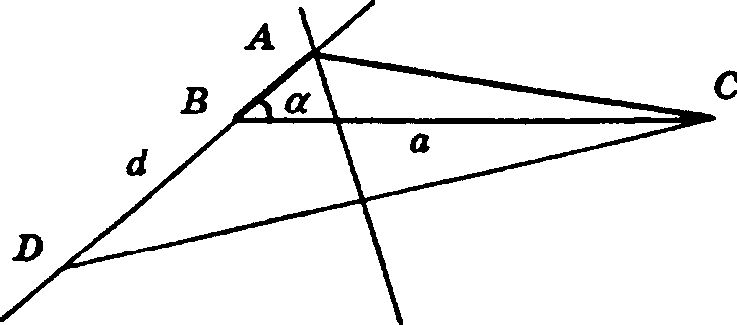
I. Допустим такой треугольник уже построен. Рассмотрим два случая:
1) ∠α — острый.
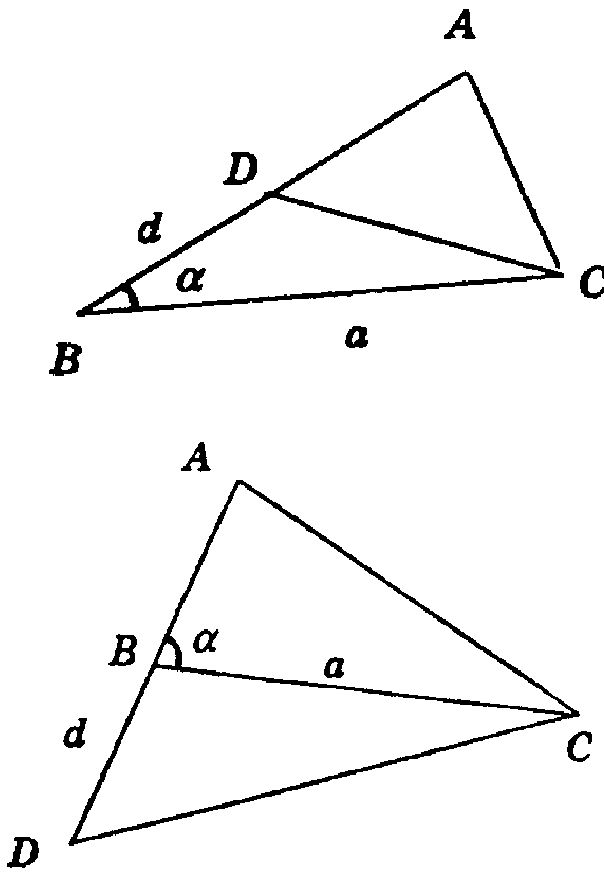
Если АВ > АС, d = АС, то отложим на стороне АВ отрезок BD = d, тогда AD = AB — d = AC, т. е. точка А лежит на серединном перпендикуляре к CD.
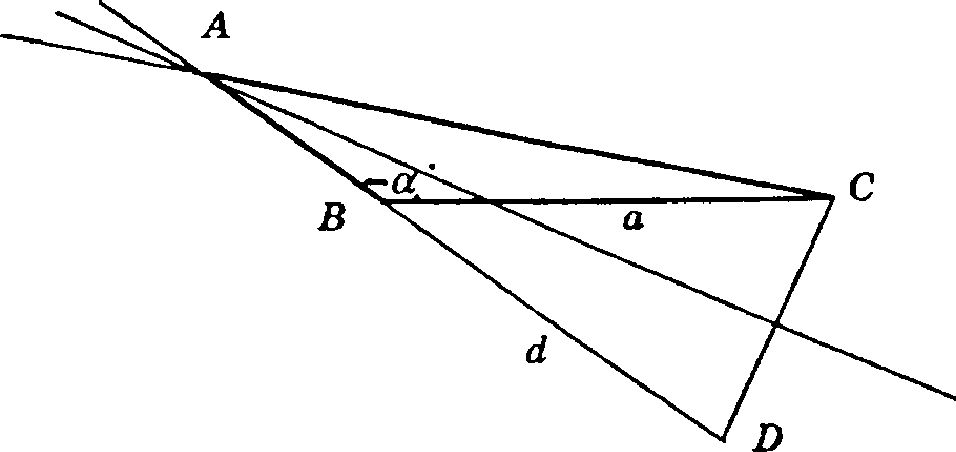
Если АС > АВ, то отложим на продолжении стороны АВ отрезок BD = d.
D = AC — AB, AD = AB + BD = AB + d, т. е. AD = AC, поэтому точка А будет лежать на серединном перпендикуляре к CD.
2) ∠α — тупой.
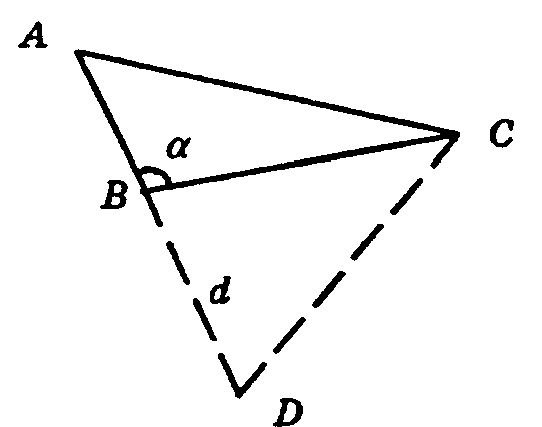
АС > АВ, тогда на продолжении сторона АВ отложим BD = d, тогда AD = AC и тогда точка А лежит на серединном перпендикуляре к CD.
А) Если α — острый угол, d = АС — АВ.
Построим ∠B = α.
Отложим на одной стороне угла ВС = а, а на дополнительной полупрямой к другой стороне BD = d.
Найдем точку А, проведя серединный перпендикуляр к стороне CD. Т. к. АВ = AD — DB = AC — d, то d = AC — AB, и ΔАВС — искомый.
Б) Если a — острый угол, d = AB — AC.
Построим ∠B = a.
Отложим на одной стороне угла ВС = а, а на другой — BD
= d.
Найдем точку А, проведя серединный перпендикуляр к отрезку CD. Т. к. ВА = d + AC, то d = AB — AC, таким образом, ΔАВС — искомый.
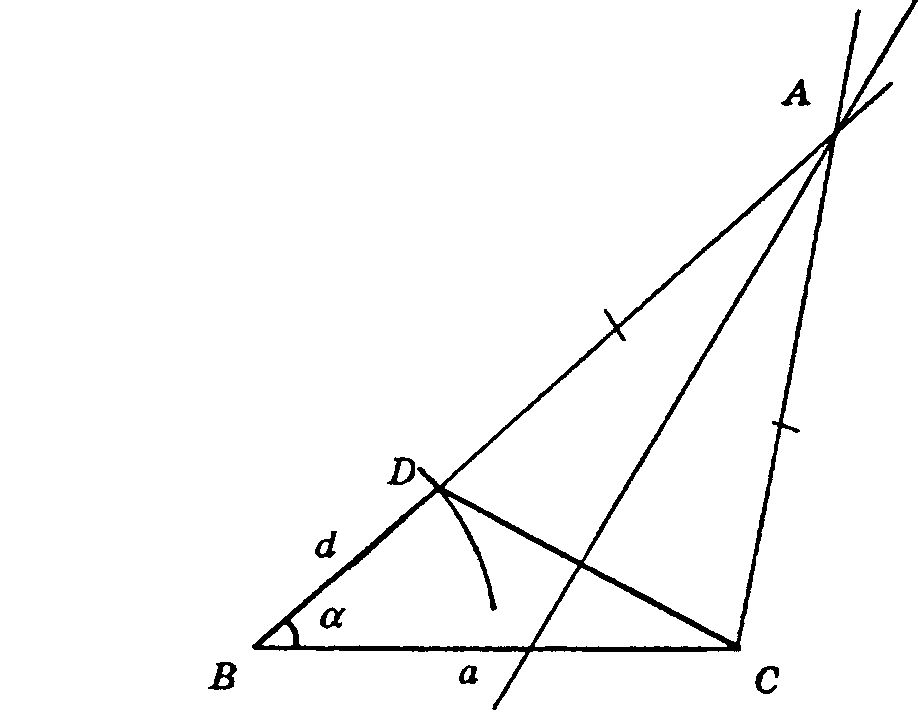
II.
Если α’ — тупой угол, то d = АС — АВ (аналогично п. I, а)
Выясним, всегда ли задача имеет решение.
I.
А) В ΔDBC ∠DBC — тупой (т. к. α и ∠DBC смежные) и DB < BC, то серединный перпендикуляр обязан пересечь сторону ВС < В и сторону ВА, таким образом, решение обязано существовать.
Б) Если ∠BDC ≤ 90°, то ∠CDA ≥ 90°. Тогда решений нет, иначе есть единственное решение.
II.
В ΔBDC ∠CBD — острый (т. к. α и ∠CBD смежные), а > d, таким образом, если ∠BDC прямой или тупой, то серединный пер
Пендикуляр к DC не пересекает сторону ВА угла СВА и, значит, решений нет. Если ∠DBC — острый, задача имеет единственное решение.
