ЛАБОРАТОРНЫЕ РАБОТЫ → номер 5
Цель работы: убедиться в том, что при движении тела по окружности под действием нескольких сил их равнодействующая равна произведению массы тела на ускорение: F = ma. Для этого используется конический маятник (рис. 178, а).
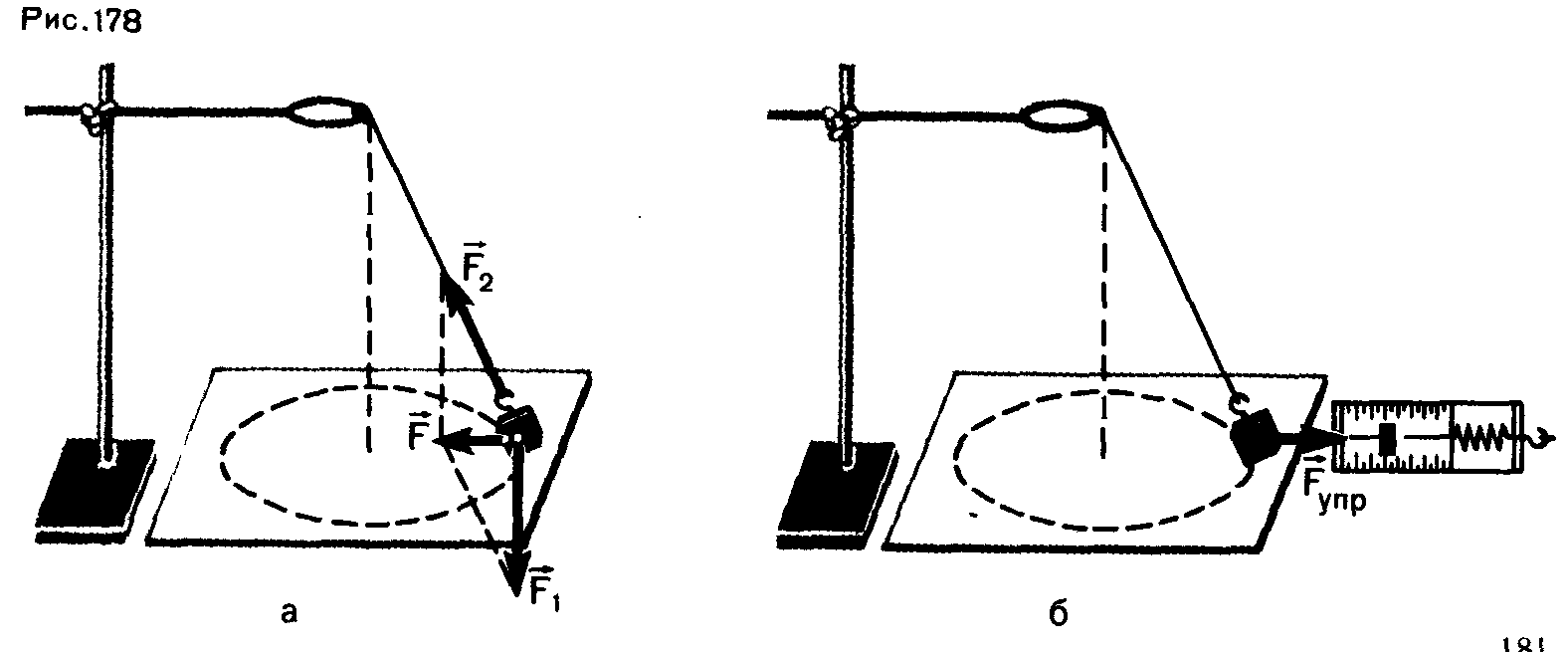
На прикрепленное к нити тело (им в работе является груз из
Набора по механике) действуют сила тяжести F1 и сила упругости F2. Их равнодействующая равна
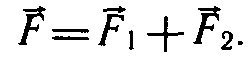
Сила F и сообщает грузу центростремительное ускорение
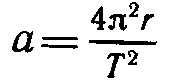
(r — радиус окружности, по которой движется груз, Т — период его обращения) .
Для нахождения периода удобно измерить время t определенного числа N оборотов. Тогда Т =
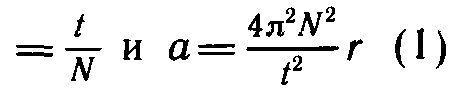
Модуль равнодействующей F сил F1 и F2 можно измерить, скомпенсировав ее силой упругости Fупр пружины динамометра так, как это показано на рисунке 178, б.
Согласно второму закону Ньютона,
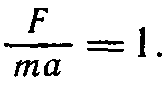
При подстановке в
Это равенство полученных в опыте значений Fynp, m и а может оказаться, что левая часть этого равенства отличается от единицы. Это и позволяет оценить погрешность эксперимента.
Средства измерения: 1) линейка с миллиметровыми делениями; 2) часы с секундной стрелкой; 3) динамометр.
Материалы: 1) штатив с муфтой и кольцом; 2) прочная нить; 3) лист бумаги с начерченной окружностью радиусом 15 см; 4) груз из набора по механике.
Порядок выполнения работы
1. Нить длиной около 45 см привяжите к грузу и подвесьте к кольцу штатива.
2. Одному из учащихся взяться двумя пальцами за нить у точки подвеса и привести во вращение маятник.
3. Второму учащемуся измерить лентой радиус r окружности, по которой движется груз. (Окружность можно начертить заранее на бумаге и по этой окружности привести в движение маятник.)
4. Определите период Т обращения маятника при помощи, часов с секундной стрелкой.
Для этого учащийся, вращающий маятник, в такт с его оборотами произносит вслух: нуль, нуль и т. д. Второй учащийся с часами в руках, уловив по секундной стрелке удобный момент для начала отсчета, произносит: «нуль», после чего первый вслух считает число оборотов. Отсчитав 30—40 оборотов, фиксирует промежуток времени t. Опыт повторяют пять раз.
5. Рассчитайте среднее значение ускорения по формуле (1), учитывая, что с относительной погрешностью не более 0,015 можно считать π2 = 10.
6. Измерьте модуль равнодействующей F, уравновесив ее силой упругости пружины динамометра (см. рис. 178, б).
7. Результаты измерений занесите в таблицу:
Номер
Опыта
T, с
Tср, с
N
M, кг
R,
М
А,
М/с2
Fупр,
Н
8. Сравните отношение
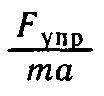
С единицей и сделайте вывод о погрешности экспериментальной проверки того, что центростремительное ускорение сообщает телу векторная сумма действующих на него сил.
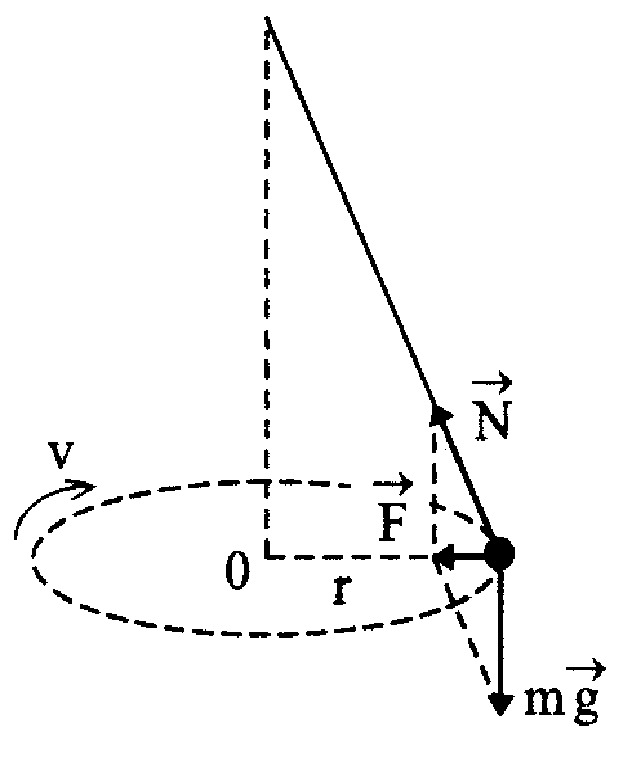
Груз из набора по механике, подвешенный на закрепленную в верхней точке нить, движется в горизонтальной плоскости по окружности радиуса r под действием двух сил:
Силы тяжести
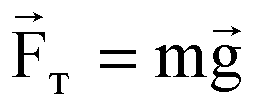
И силы упругости N.
Равнодействующая этих двух сил F направлена горизонтально к центру окружности и сообщает грузу центростремительное ускорение.
Т — период обращения груза по окружности. Его можно вычислить подсчитав время, за которое груз совершает некоторое число полных оборотов
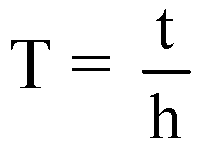
Центростремительное ускорение рассчитаем по формуле
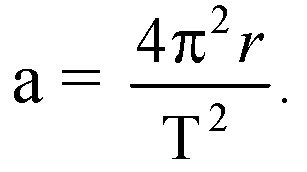
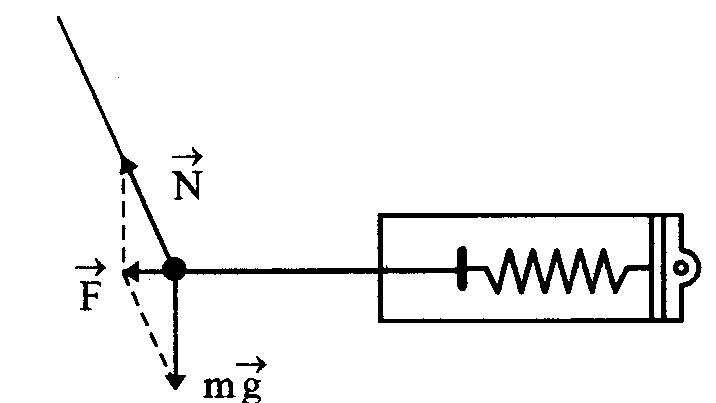
Теперь, если взять динамометр и прикрепить его к грузу, как показано на рисунке, можно определить силу F (равнодействующую сил mg и N.
Если груз отклонен от вертикали на расстояние г, как и при движении по окружности, то сила F равна той силе, которая вызывала движение груза по окружности. Мы получаем возможность сравнить значение силы F, полученное путем прямого измерения и силы ma, рассчитанной по результатам косвенных измерений и
Сравнить отношение
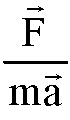
С единицей. Для того, чтобы радиус окружности, по которой движется груз, изменялся вследствие влияния сопротивления воздуха медленнее и изменение это незначительно влияло на измерения, следует выбирать его небольшим (порядок 0,05~0,1 м).
Выполнение работы
№ опыта
T, с
Tср, с
N
M, кг
R, м
А, м/с2
F, H
Вычисления
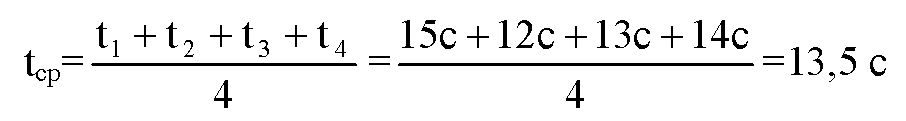
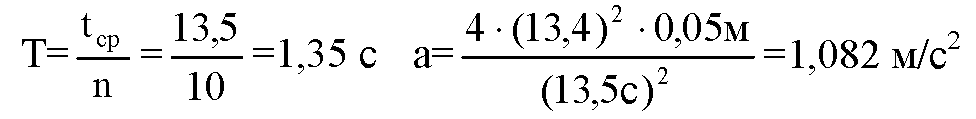
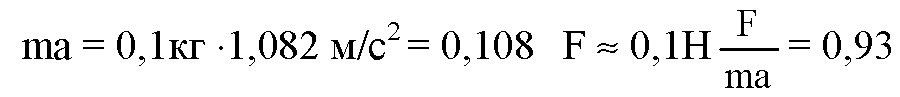
Оценка погрешностей. Точность измерения: линейка —
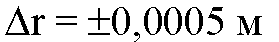
Секундомер
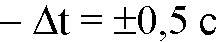
Динамометр
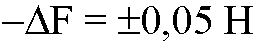
Подсчитаем погрешность определения периода (если считать, что число n определено точно):
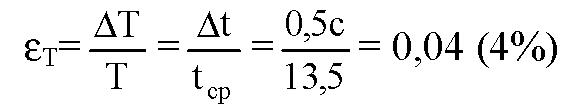
Погрешность определения ускорения подсчитаем как:
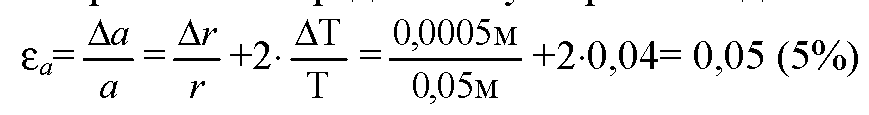
Погрешность определения ma
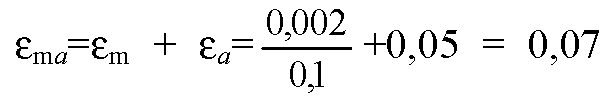
(7%), то есть
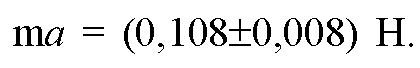
С другой стороны, силу F мы измерили со следующей погрешностью:
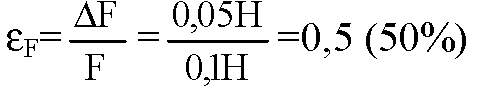
Такая погрешность измерения, конечно, очень велика. Измерения с такими погрешностями годны только для приблизительных оценок. Отсюда видно, что отклонение отношение
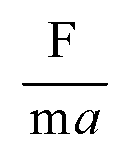
От единицы может быть существенным при использовании примененных нами способов измерения*.
1* Так что вам не следует смущаться, если в этой лабораторной работе отношение
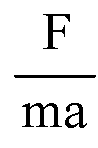
Будет отличным от единицы. Просто аккуратно оцените все погрешности измерений и сделайте соответствующий вывод.
