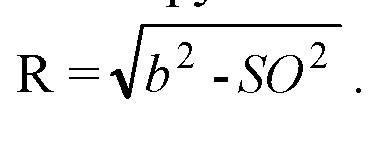§17. Перпендикулярность прямых и плоскостей → номер 22
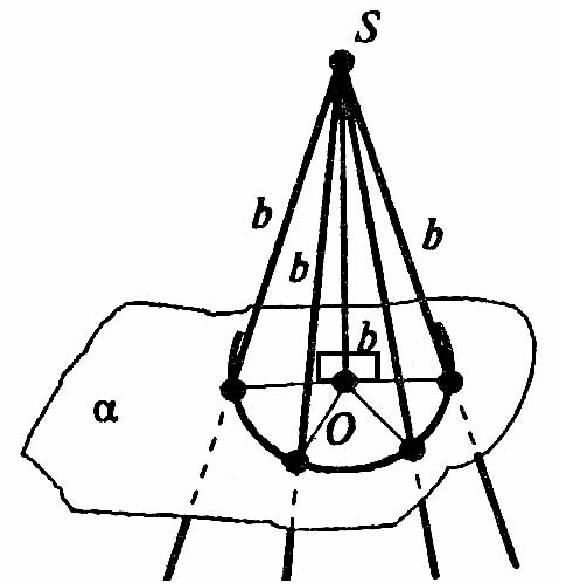
Пусть S — данная точка, SO — перпендикуляр к плоскости α, b — длина наклонных. Поскольку каждая наклонная из точки S имеет одинаковую длину, то расстояния от точки О до оснований всех наклонных будут одинаковы. Поэтому искомое геометрическое место точек — это окружность в данной плоскости с центром в
Точке О и радиусом