4. Даны три различные попарно пересекающиеся плоскости. Докажите, что если две из прямых пересечения этих плоскостей пересекаются, то третья прямая проходит через точку их пересечения

§15. Аксиомы стереометрии и их простейшие следствия → номер 4

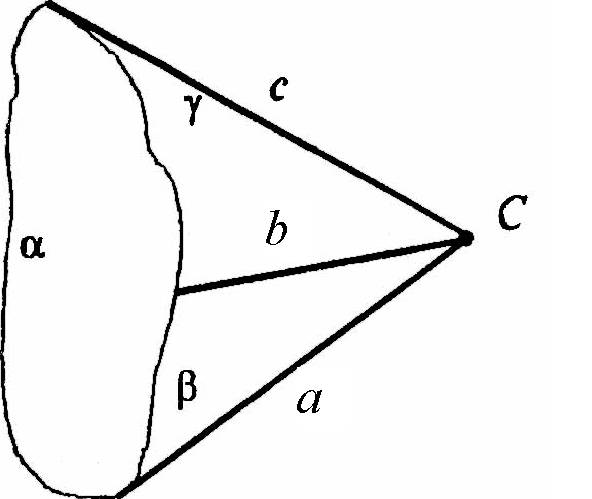
Допустим плоскости α и β пересекаются по прямой а, а плоскости β и γ — по прямой b, причем прямые а и b пересекаются в точке С. Тогда по аксиоме 2 точка C принадлежит всем трем плоскостям α, β и γ а значит, и третьей прямой с пересечения плоскостей α и γ. Что и требовалось доказать.