Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 151
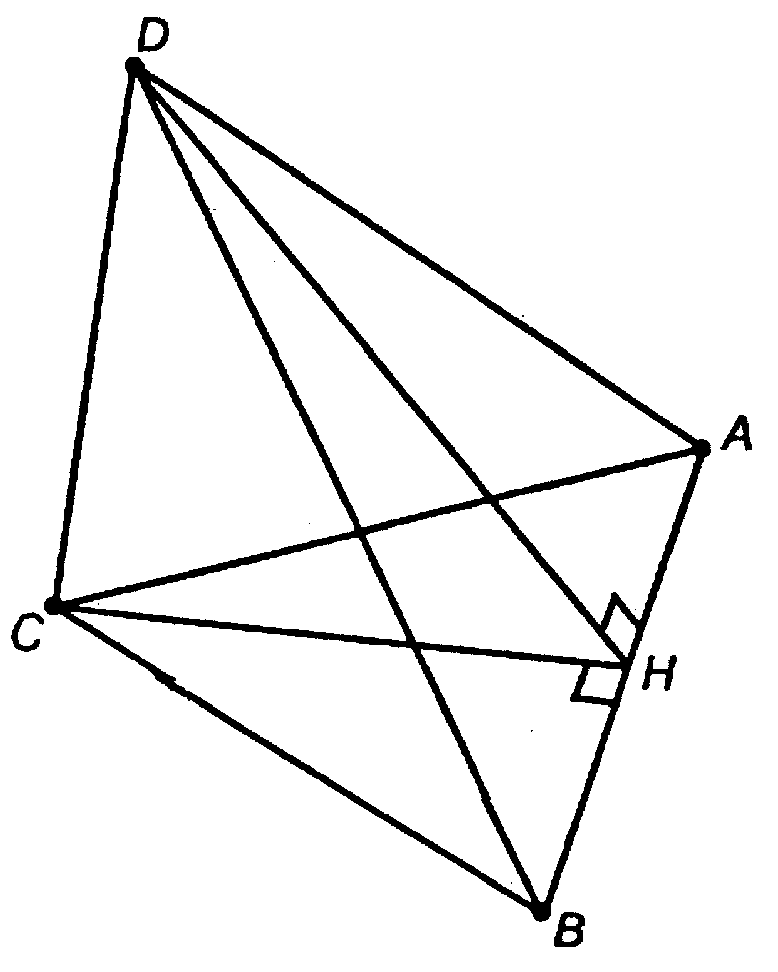
Дано: CD ⊥ (АВС); DH — высота в ABD.
Решение:
Найдем проекцию границы ΔABD на (ABC).
Проекция DB на (АВС) — отрезок СВ; проекция DA на (АВС) — отрезок АС. АВ является своей проекцией.
Т. о. проекция границы ΔDAB на пл. АВС есть стороны ΔАВС, внутренние точки ΔDAB проектируются во внутренние точки ΔАВС, тогда ΔАВС есть проекция ΔDAB на плоскость АВС.
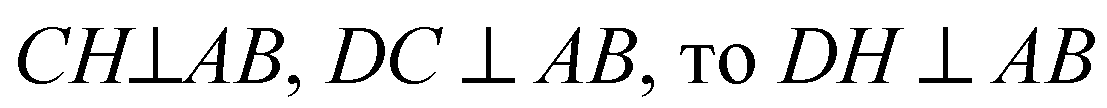
(теорема о 3-х перпендикулярах).
Таким образом, DH — высота ΔDAB. Что и требовалось доказать.
