Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 158
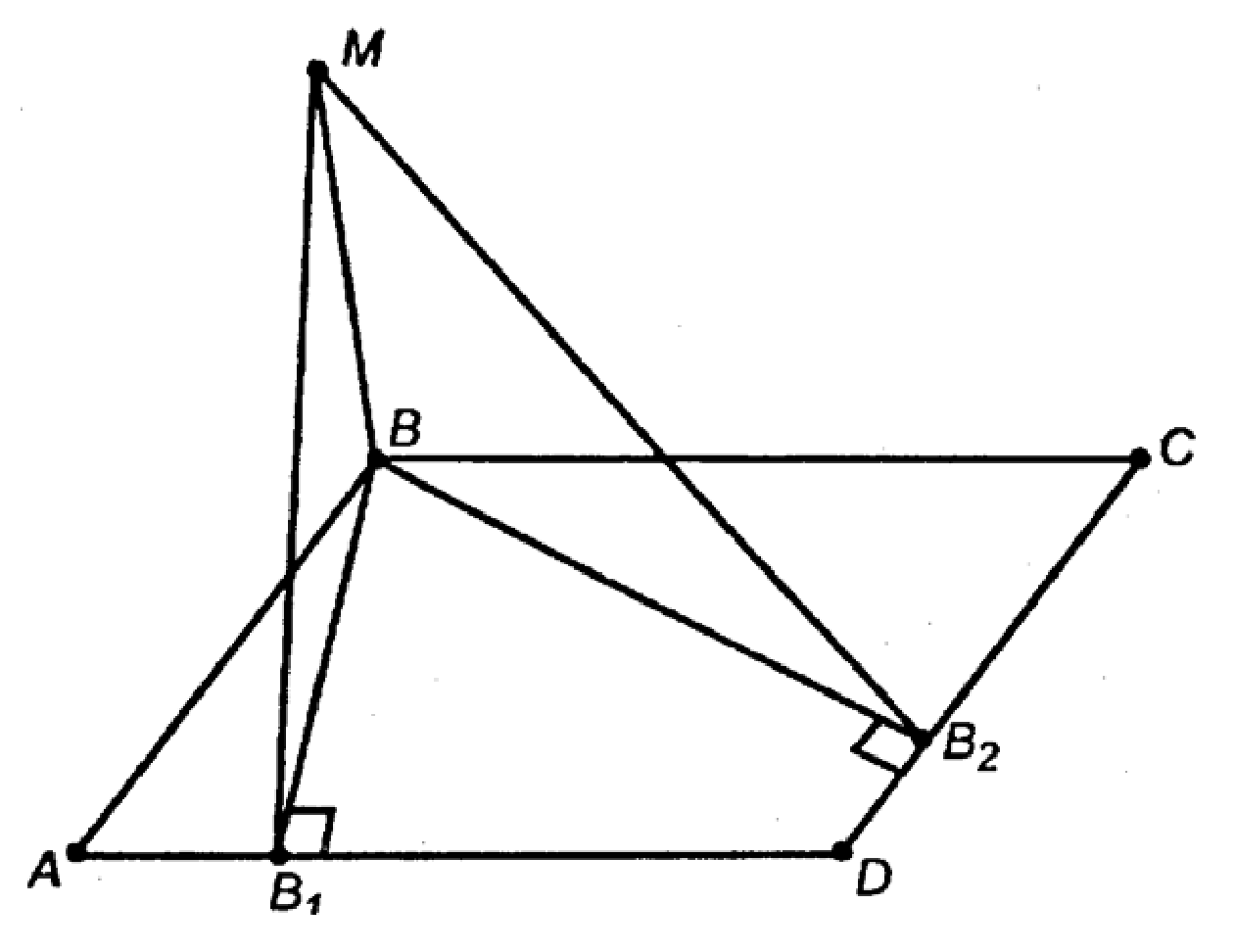
Дано: ABCD — ромб;
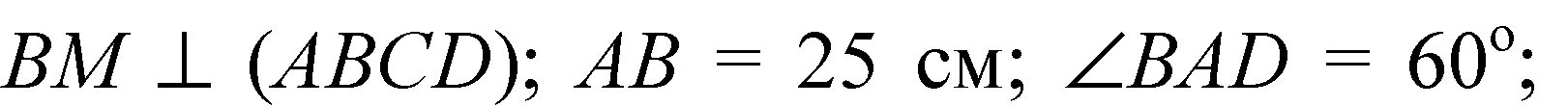
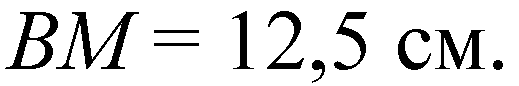
Решение:
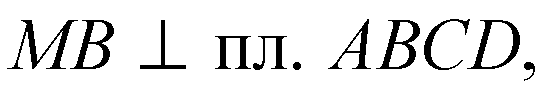
Следовательно,
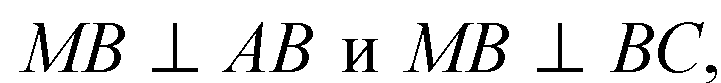
Следова
Тельно,
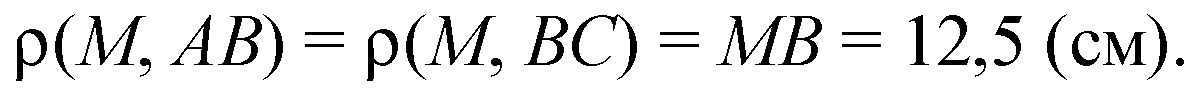
Проведем в пл. ABCD отрезки ВВ1 ⊥ AD и ВВ2 ⊥ CD.
По теореме о 3-х перпендикулярах МВ1 ⊥ AD и МВ2 ⊥ DC.
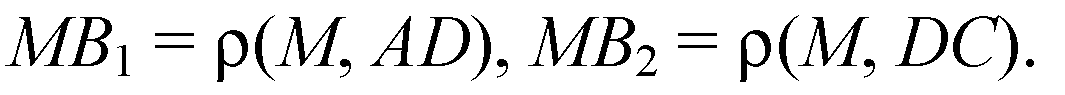
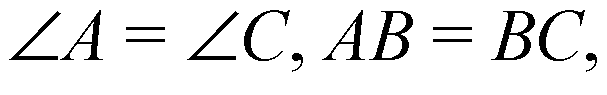
Поэтому
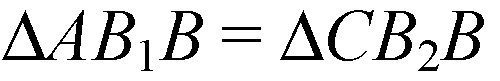
(т. к. ABCD — ромб).
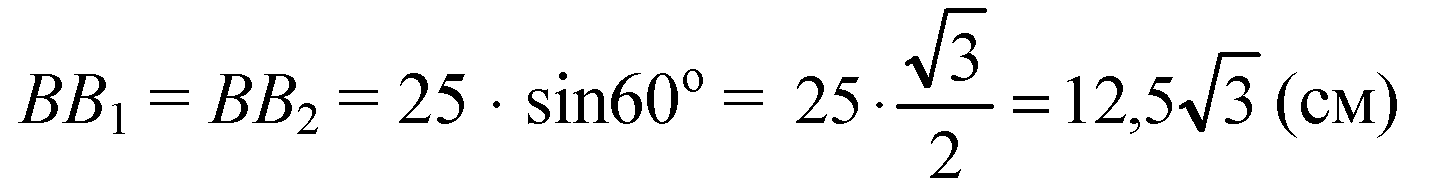
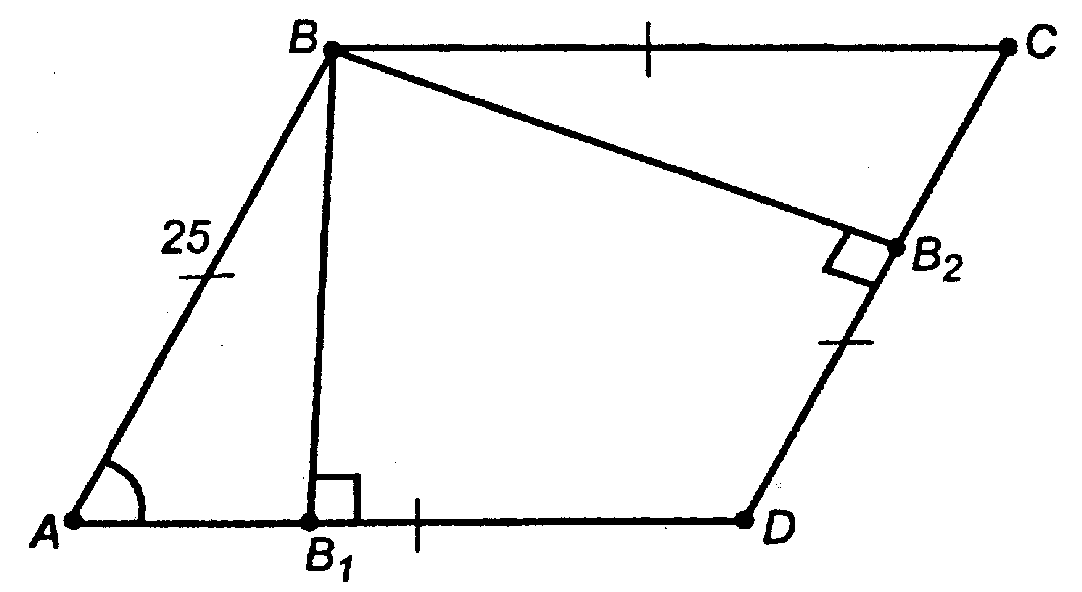
МВ2 и МВ1 — наклонные, их проекции (ВВ1 и ВВ2) равны, значит, и сами наклонные равны, то есть МВ1 = МВ2.
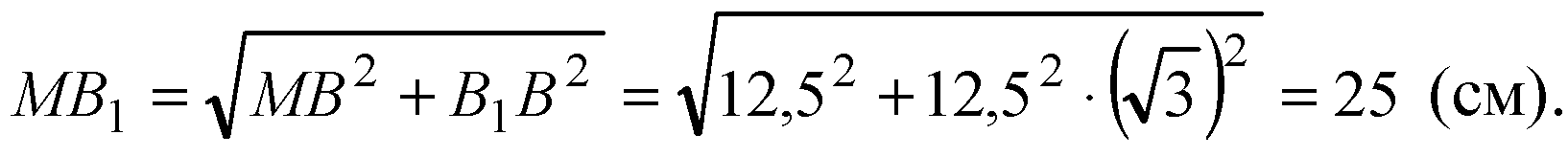
Ответ: