179. Плоскости α и β; взаимно перпендикулярны. Через некоторую точку плоскости α проведена прямая, перпендикулярная к плоскости β;. Докажите, что эта прямая лежит в плоскости α

Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 179

* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.

Дано:

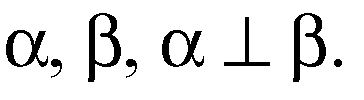
Решение:

Пусть АВ ⊄ α (где АВ — перпендикуляр β, проведенный через А ∈ α).

DE — линия пересечения α и β.

Проведем в пл. α АС ⊥ DE, a в пл. β (через построенную т. С) CF ⊥ DE.

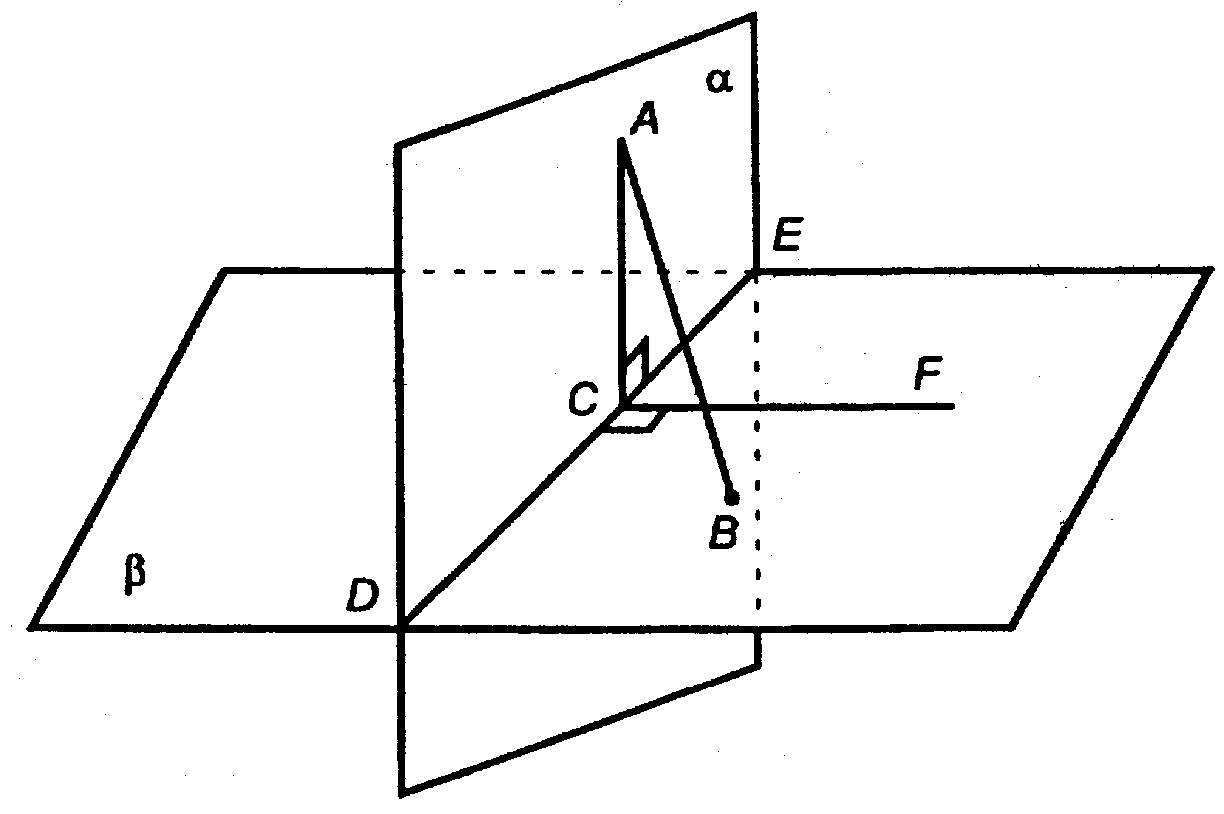
∠ACF — линейный угол двугранного угла ADEF, ∠ACF = 90o.

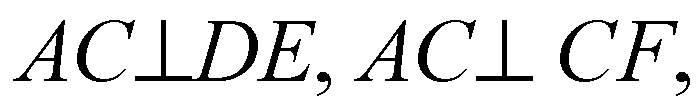
То

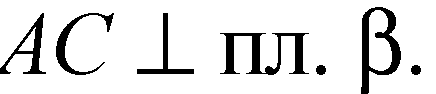
Из точки А проведены 2 различных перпендикуляра к пл. β, что невозможно.

Наше допущение неверно,

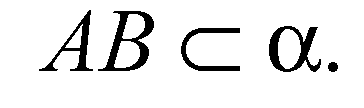
Что и требовалось доказать.