Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 186
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Решение. Рассмотрим плоскость α, проходящую через прямую а и параллельную прямой b. Через прямые а и b проведем плоскости β и γ так, чтобы β⊥α и γ⊥α (задача 185). Докажите самостоятельно, что прямая р, по которой пересекаются плоскости β и &gamma, является искомой.
Докажем, что р — единственная прямая, удовлетворяющая условию задачи. Предположим, что существуют две прямые А1В1 и А2В2, пересекающие данные скрещивающиеся прямые а и b и перпендикулярные к каждой из них (рис. 65). Прямые А1В1 и А2В2 перпендикулярны к плоскости α (объясните почему), поэтому они параллельны. Отсюда следует, что скрещивающиеся прямые а и b лежат в одной плоскости, что противоречит определению скрещивающихся прямых. 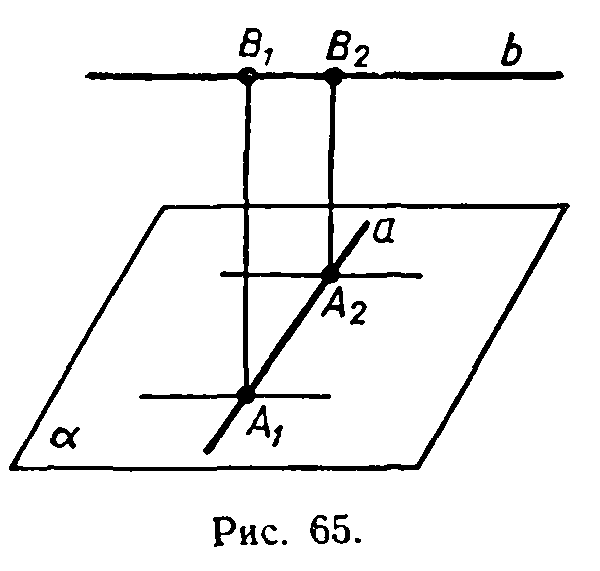
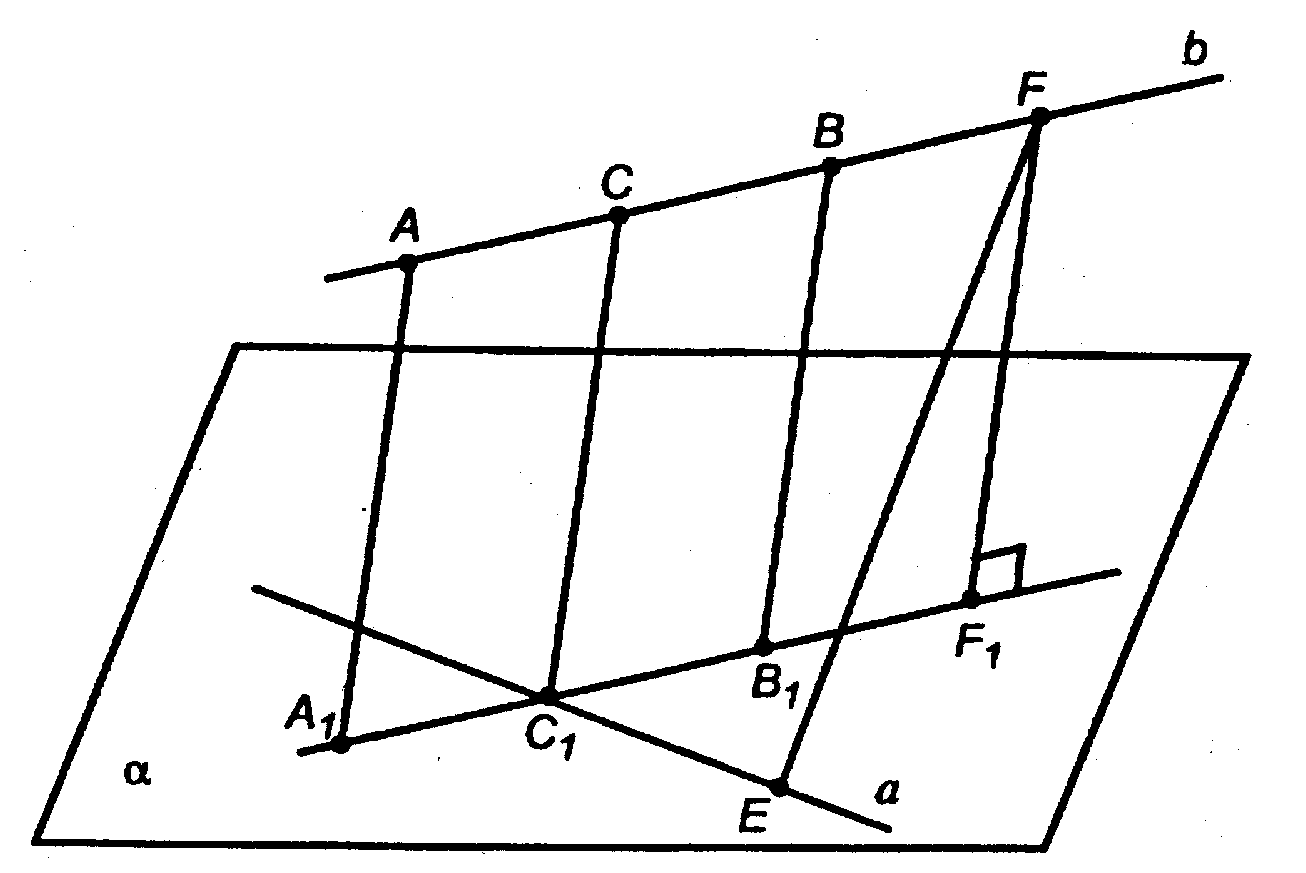
Альтернативное Решение:
По условию даны скрещивающиеся прямые а и b. Построим прямую, пересекающую обе данные прямые и перпендикулярную к ним.
Проведем через прямую а. α || b. Из произвольных точек А ∈ b, B ∈ b проведем АА1 ⊥ α и ВВ1 ⊥ α. Соединим А1 и В1 отрезком и найдем точку С1 пересечения прямых А1В1 и а. Через т. С1 проведем прямую, перпендикулярную α. Эта прямая:
1) пересекается с прямой b в некоторой точке С
(плоскости А1АВВ1 и α взаимно перпендикулярны; через
Т. С1 ∈ пл. А1АВВ1 проведена прямая, перпендикулярная α. Эта прямая будет лежать в пл. А1АВВ1 (Это доказано в задаче 179).
Эта прямая
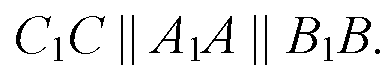
С1С пересечет b);
2)
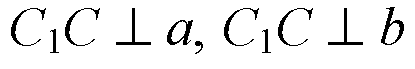
(раз
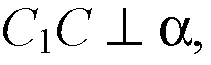
То
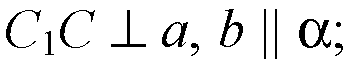
По теореме II
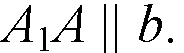
Раз
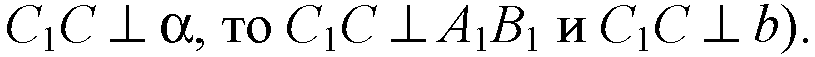
Прямая С1С — искомая.
Отрезок С1С меньше всех других отрезков, которые можно получить, соединяя точки прямой а с точками прямой b. Например, возьмем т. Е ∈ а, т. F ∈ b, проведем отрезок EF и докажем, что EF > C1C.
Проведем
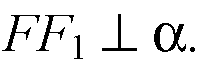
Тогда
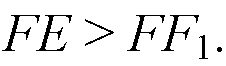
Но
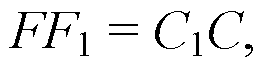
Следовательно,
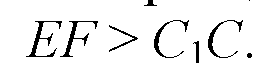
Вывод: С1С — единственная, т. к. все остальные отрезки длиннее СС1, поэтому не могут являться общим перпендикуляром к а и b (т. к. это кратчайшее расстояние).
Что и требовалось доказать.
