Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 195
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
195. Найдите измерения прямоугольного параллелепипеда ABCDA1B1C1D1, если АС1 = 12 см и диагональ BD1 составляет с плоскостью грани AA1D1D угол в 30°, а с ребром DD1 — угол в 45°.
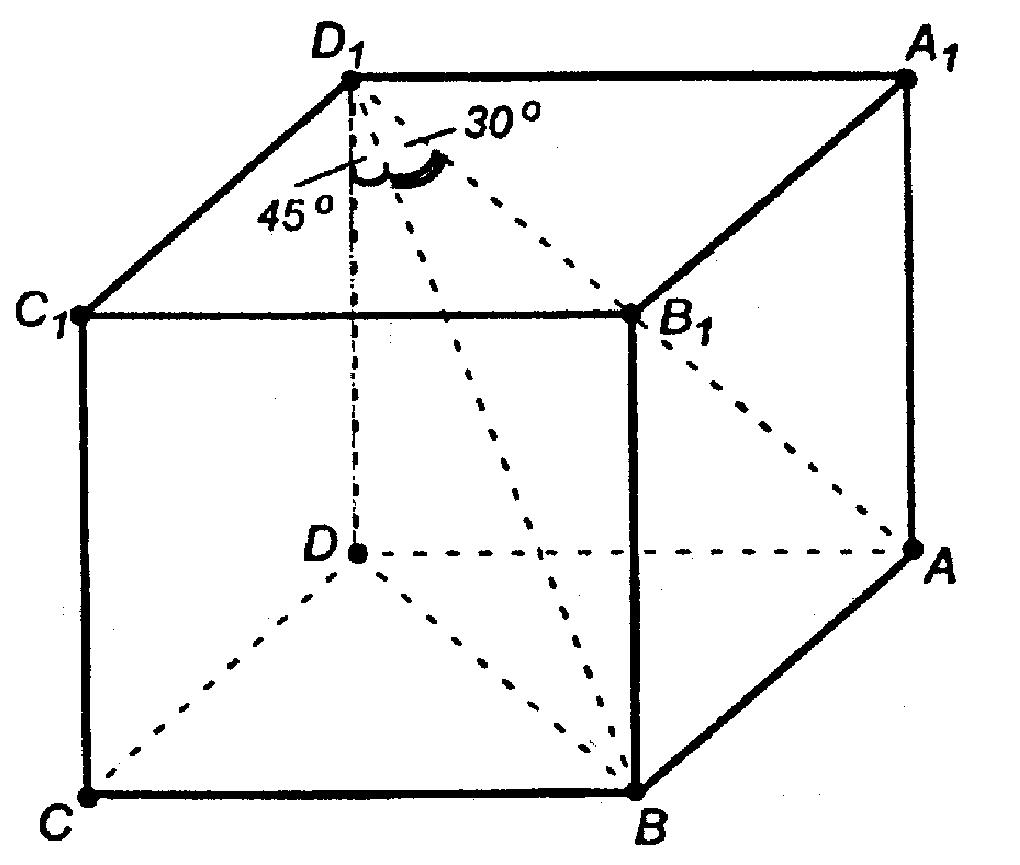
Дано:
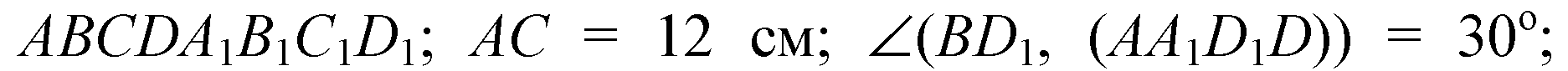
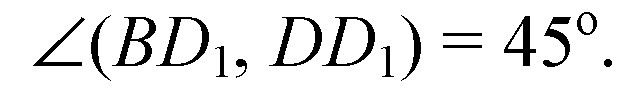
Решение:
АВ ⊥ пл. АА1D1D, поэтому отрезок AD1 есть проекция BD1 на плоскость грани AA1D1D.
Так как диагонали прямоугольного параллелепипеда равны, то
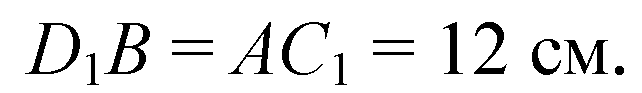
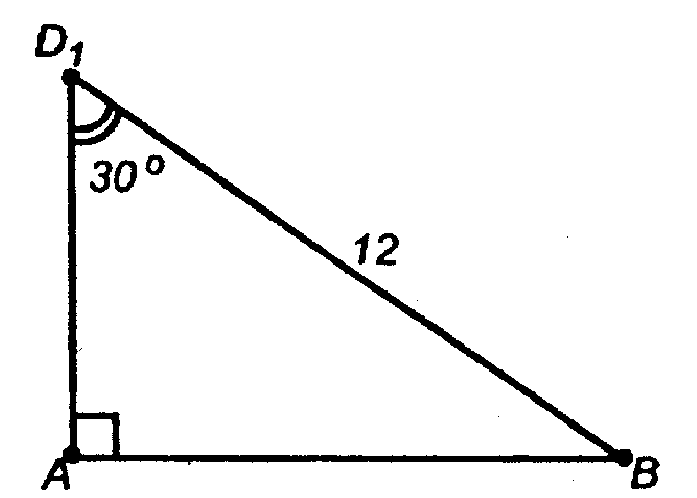
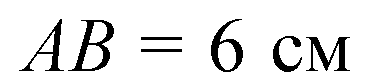
(т. к. он лежит против угла 30о, то равен половине ги
Потенузы).
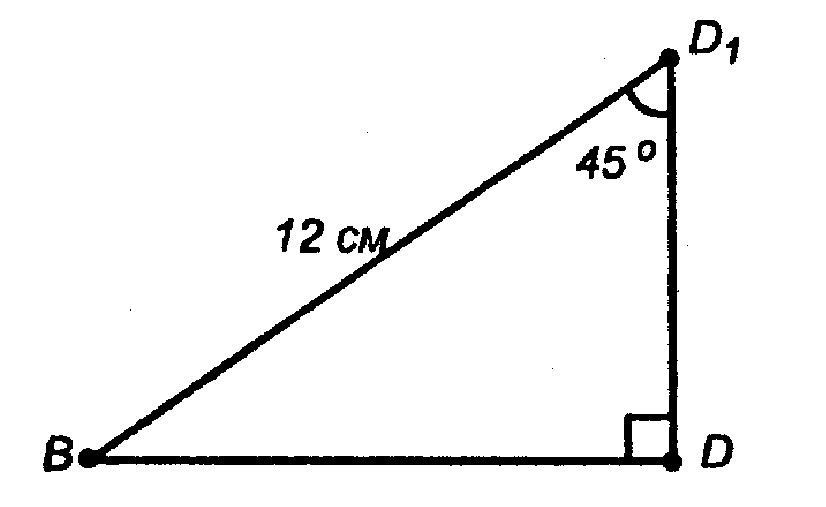
Из ΔBDD1 — прямоугольного:
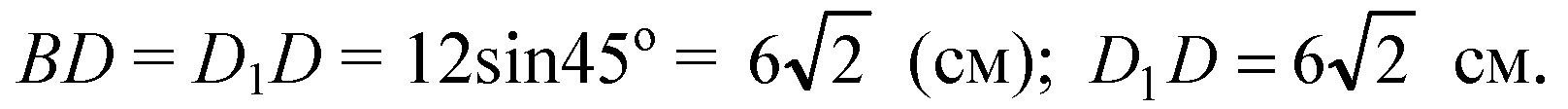
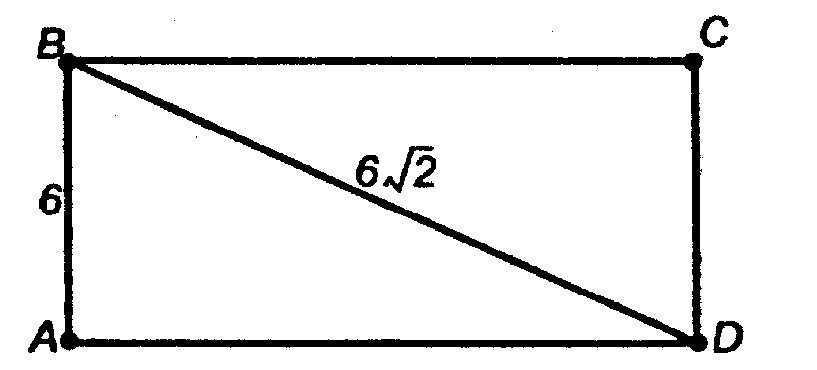
По теореме Пифагора:
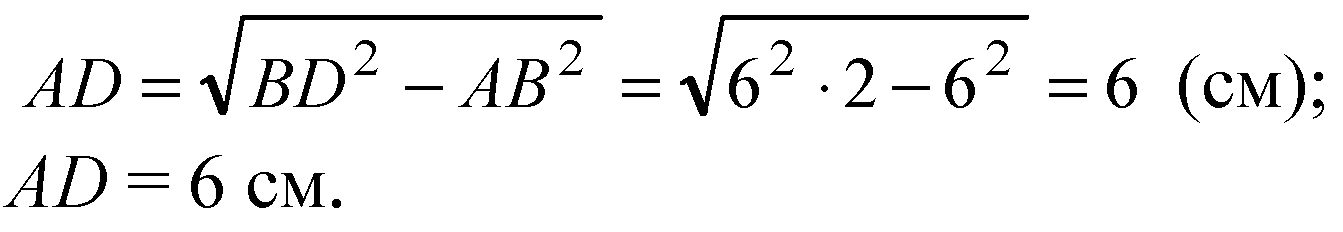
Ответ: