Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 196
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
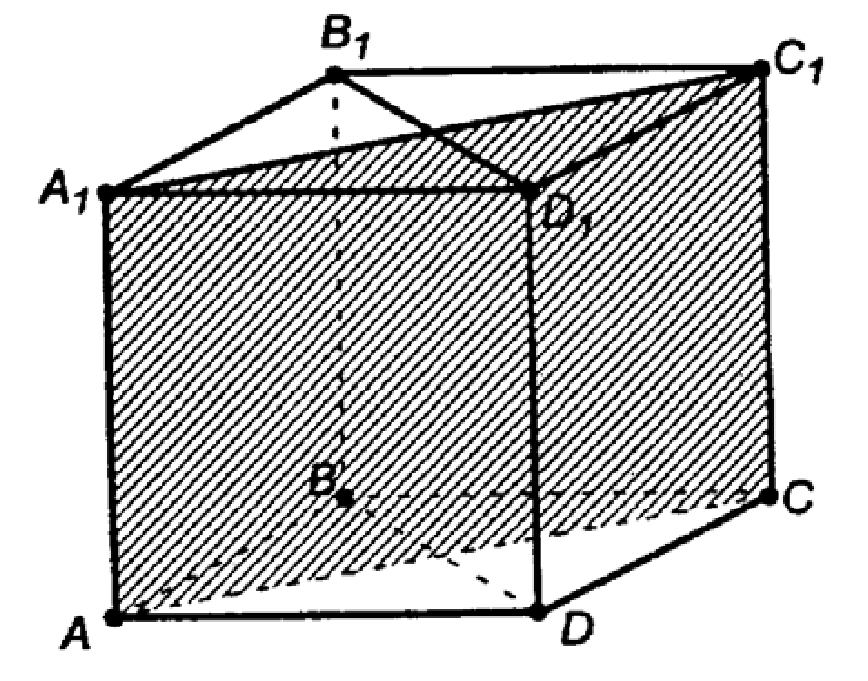
196. Изобразите куб ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через: а) ребро АА1 и перпендикулярной к плоскости BB1D1; б) ребро АВ и перпендикулярной к плоскости CDA1.
Решение:
А) АС ⊥ BD — по свойству диагоналей квадрата (они перпендикулярны).
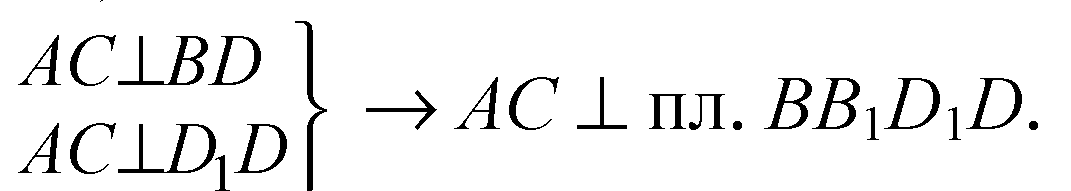
Так как пл. АА1С1С проходит через АС, то пл. АА1С1С ⊥ пл. BB1D1D. Плоскость АА1С1С — искомое сечение.
Б)
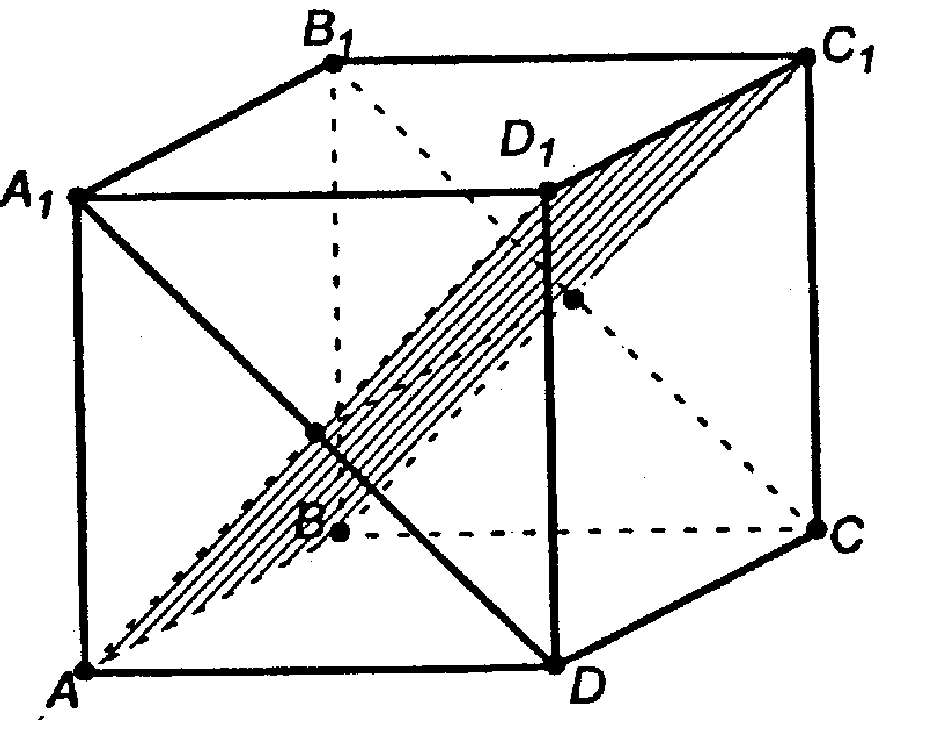
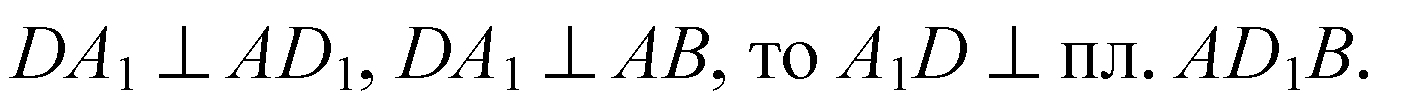
Плоскости ABC1D1 и A1B1CD — перпендикулярны (т. к. A1B1CD проходит через прямую A1D ⊥ пл. AD1B).
4-угольник ABC1D1 — искомое сечение.
