Дополнительные задачи к главе II Перпендикулярность прямых и плоскостей. → номер 201
Решение:
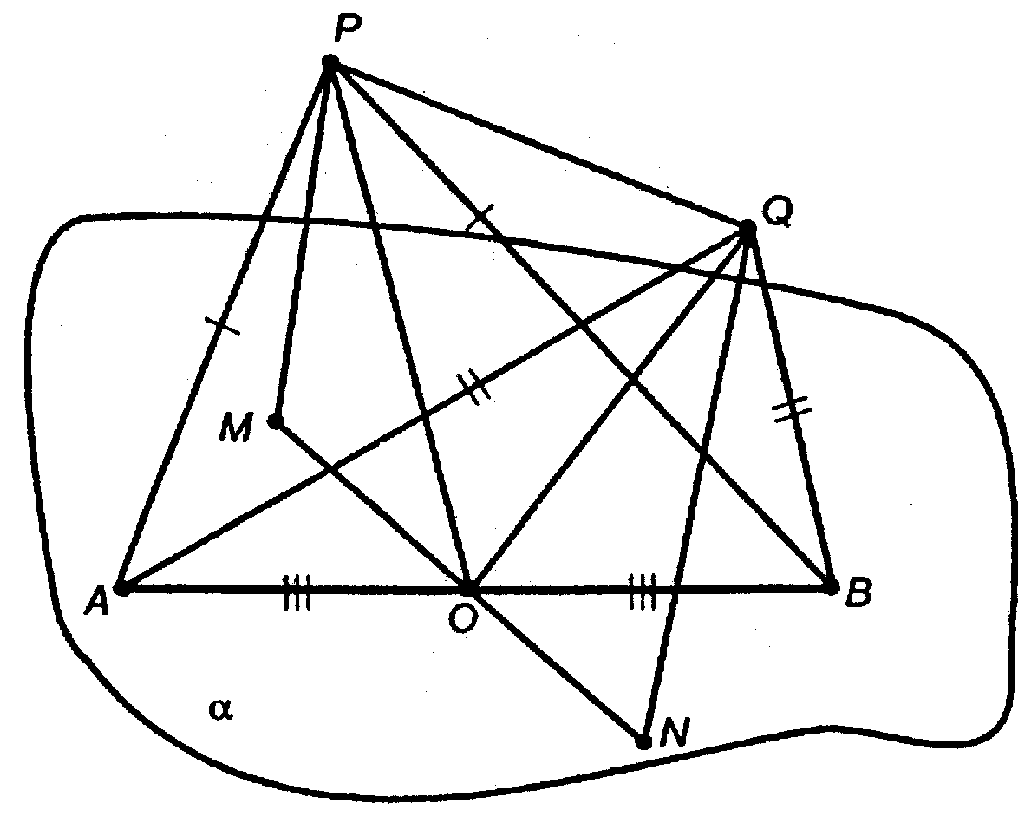
1. Проведем РМ ⊥ α и QN ⊥ α; через середину АВ точку О — проведем отрезки OQ и ОР, соединим точки О и N, О и М.
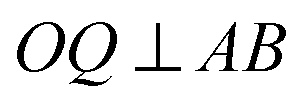
— по свойству медианы в равнобедренном ΔABQ.
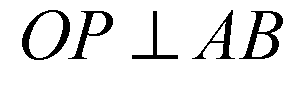
— по свойству медианы в равнобедренном ΔАВР.
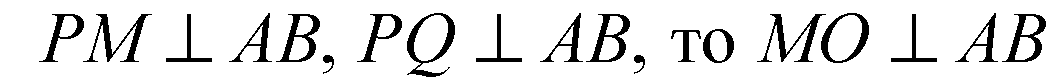
По теореме, обратной к теореме
О 3-х перпендикулярах;
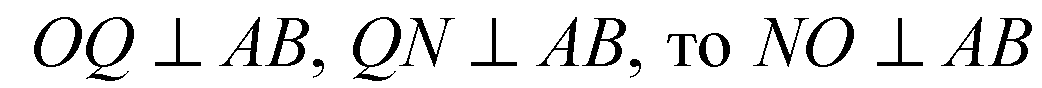
По теореме, обратной к теореме
О 3-х перпендикулярах.
В α через т. О к отрезку АВ можно провести единственный перпендикуляр, поэтому точки М, О, N лежат на одной прямой MN.
PM || QN, через них можно провести единственную плоскость MPQN, АВ ⊥ пл. MPQN.
Рассмотрим два случая:
Случай I. PQ || a.
Тогда
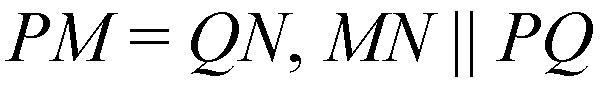
И угол между PQ и АВ равен углу меж
Ду MN и АВ. А угол между MN и АВ равен 90о.
Случай II. Продолжение PQ пересекает плоскость α.
Тогда MN есть проекция продолженного отрезка PQ на пл. α.
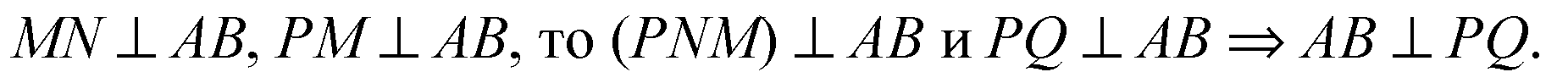
Ответ: 90о.
