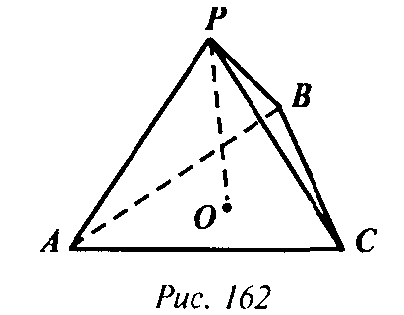Глава III Многогранники. § 2. Пирамида → номер 247 247. Двугранные углы при основании пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр окружности, вписанной в основание; б) высоты всех боковых граней, проведенные из вершины пирамиды, равны; в) площадь боковой поверхности пирамиды равна половине произведения периметра основания на высоту боковой грани, проведенную из вершины.
Указание: при обозначениях как в задаче 246 доказать, что ΔPOA1 = ΔРОВ1 = ΔPOC1 откуда непосредственно следует п. а) и п. б), п. в).