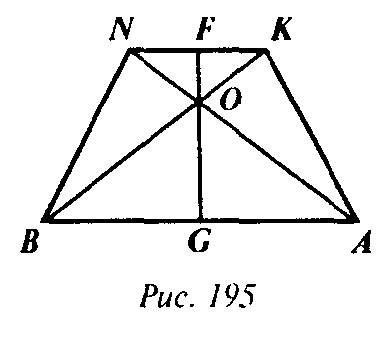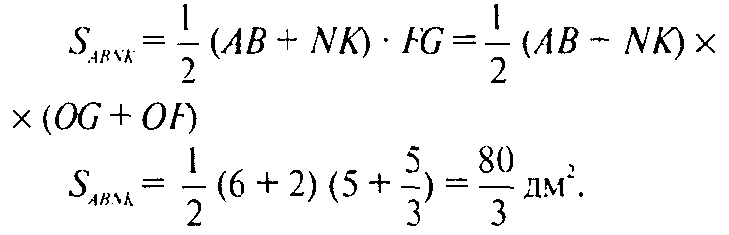Глава III Многогранники. Дополнительные задачи → номер 309
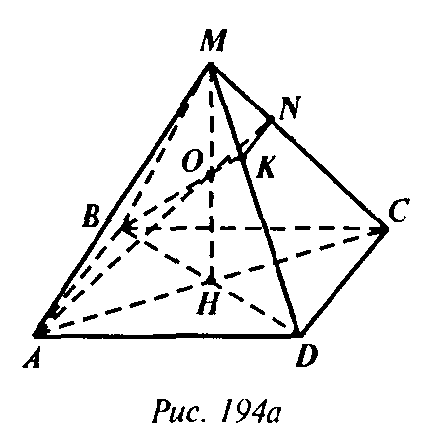
Пусть МН — высота пирамиды MABCD. О — середина МН. Проведем сечение через сторону АВ = 6 дм и точку О. Так как точки А, O, H, M, С лежат в одной плоскости MAC, то прямая АО лежит и в плоскости сечения и в плоскости MAC. Поэтому точка N— точка пересечения АО и MC, также лежит в плоскости сечения. Аналогично точка К— точка пересечения ВО и MD тоже принадлежит сечению. Таким образом ABNK— искомое сечение (рис. 194а).
Докажем, что
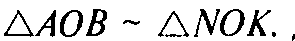
Действительно:
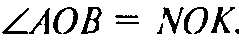
Докажем, что
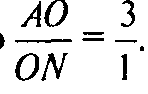
Рассмотрим
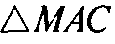
(рис. 194б). Проведем OO’ — среднюю линию ΔMHC и ОЕ — параллельно АС. Тогда из того, что
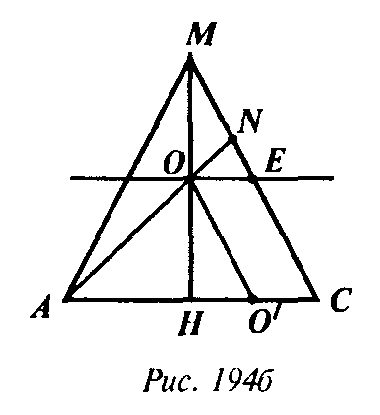
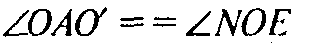
И
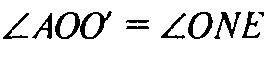
Следует, что
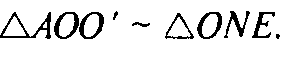
Значит
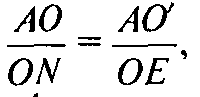
Но
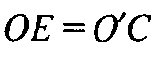
(так как ОЕСО’ — параллелограмм), а
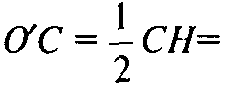
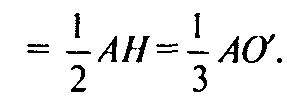
Поэтому
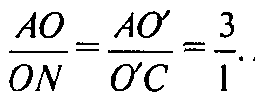
Аналогично рассматривая ΔMBD получаем, что
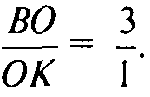
Поэтому
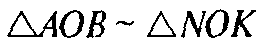
И коэффициент подобия равен 3. Так как АВ = 6 дм, то NK = 2 дм. Очевидно, что АВ || NK. Поэтому ABNK — трапеция. Проведем высоту FOG трапеции ABNK через точку О (рис. 195).
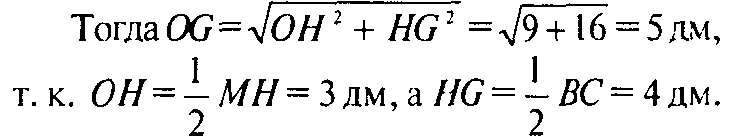
Тогда из подобия треугольников AOB и NOK следует, что
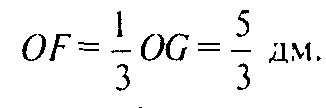
Таким образом: