Глава III Многогранники. Дополнительные задачи → номер 318
1) Найдем косинус двугранного угла тетраэдра: Пусть ребро тетраэдра DABC равно а. Проведем высоту DH и апофему DM грани DAC. Тогда ∠DMH — линейный угол двугранного угла правильного тетраэдра.
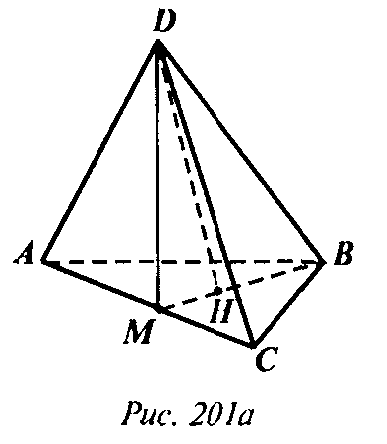
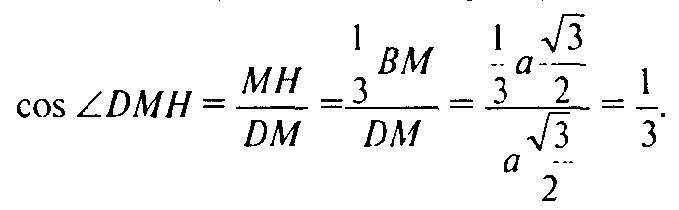
Таким образом
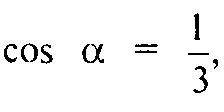
Где а — двугранный угол тетраэдра. 2) Найдем косинус половины двугранного угла правильного октаэдра MABCDN:
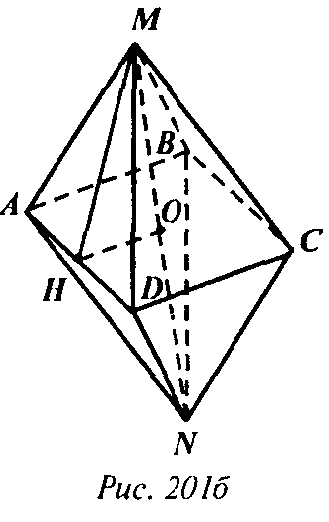
Проведем апофему МН грани MAD и пусть MN пересекает плоскостью ABCD в точке О. Тогда точка О — точка пересечения диагоналей квадрата ABCD и МО⊥ABCD. Поэтому
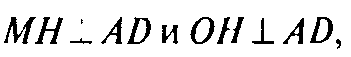
Следовательно, ∠MHO — линей ный угол двугранного угла
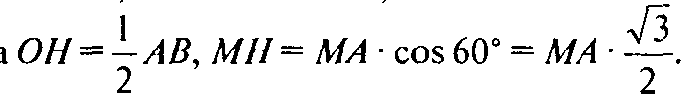
Таким образом
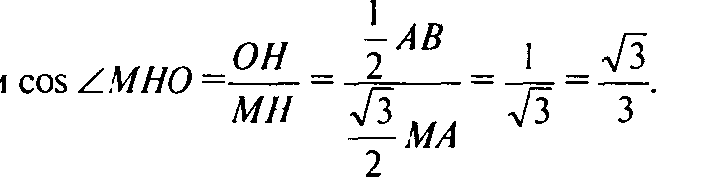
Таким образом
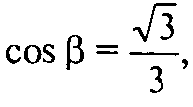
Где β — половина двугранного угла правильного октаэдра. Тогда α + 2β — сумма двугранных углов тетраэдра и октаэдра.
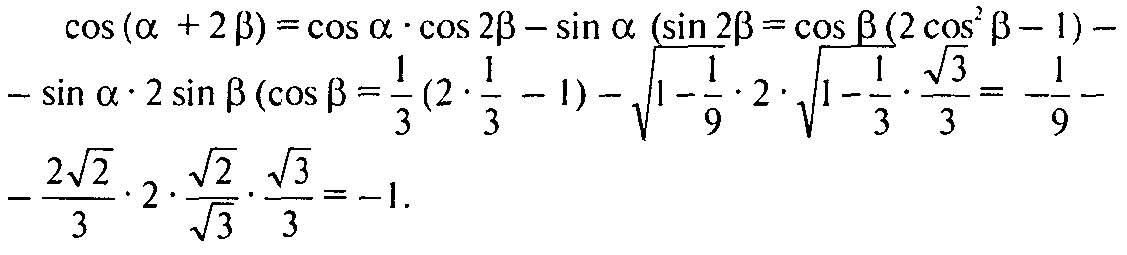
Поэтому
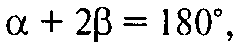
Что и требовалось доказать.
