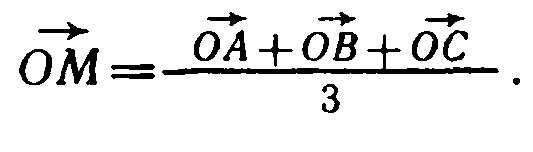Глава IV. Векторы в пространстве § 3. Компланарные вектора → номер 366
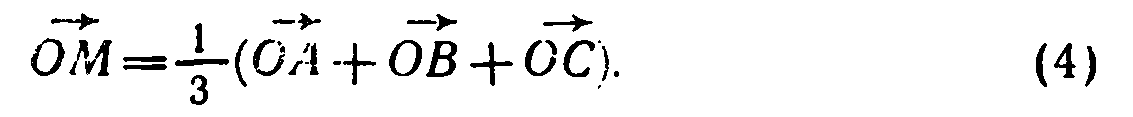
Решение. По теореме о точке пересечения медиан треугольника АМ — 2МА1, где АА1—медиана треугольника ABC (рис. 110). Согласно задаче 349 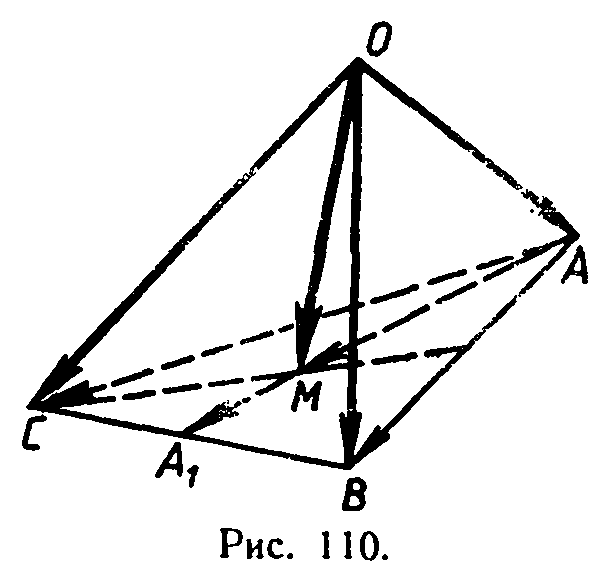
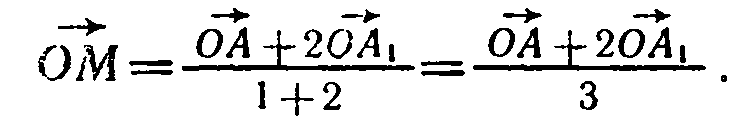
Но
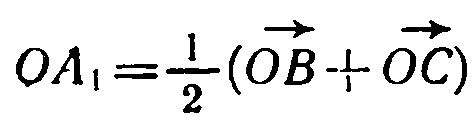
(объясните почему), поэтому
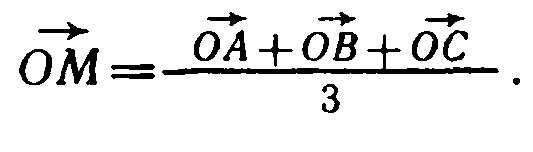
Глава IV. Векторы в пространстве § 3. Компланарные вектора → номер 366
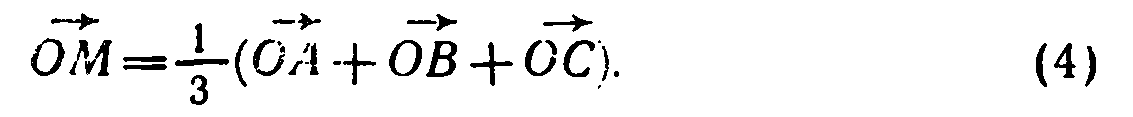
Решение. По теореме о точке пересечения медиан треугольника АМ — 2МА1, где АА1—медиана треугольника ABC (рис. 110). Согласно задаче 349 
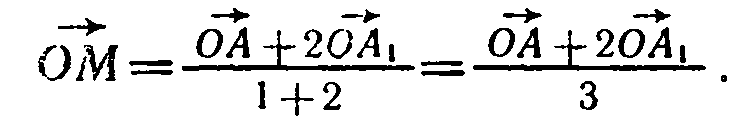
Но
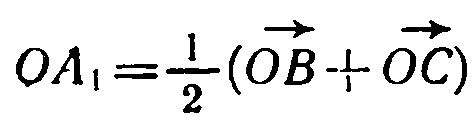
(объясните почему), поэтому