Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 421
Р е ш е н и е. а) Если векторы АВ и АС коллинеарны, то точки A, В и С лежат на одной прямой, а если не коллинеарны, то точки A, В и С не лежат на одной прямой. Найдем координаты этих векторов: АВ { — 8; 11; —7}, AC{24; —33; 21}.
Очевидно, АС = —3АВ, поэтому векторы АВ и АС коллинеарны, и, следовательно, точки Л, В и С лежат на одной прямой.
а) Если векторы AB и AC коллинеарны, то точки А, В и С лежат на одной прямой, а если не коллинеарны, то точки А, В и С не лежат на одной прямой. Вычислим координаты этих векторов:
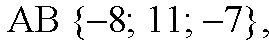
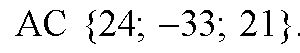
Заметим, AC=-3АВ, следовательно, векторы AB и АС коллинеарны, т. е. точки A, В и С лежат на одной прямой. б) Найдем координаты векторов AB и AC. AB
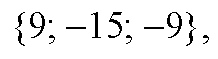
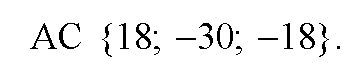
Очевидно, что AC=2⋅AB, поэтому векторы AB и AC коллинеарны, значит точки А, В, и С лежат на одной прямой.
В) Найдем координаты векторов AB и AC.
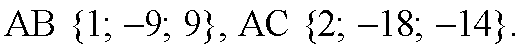
Векторы AB и AC не коллинеарны, значит, точки A, B и С не лежат на одной прямой.
