Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 422
Рассмотрим векторы DA, DB, DC. а) Вычислим координаты векторов DA, DB и DC:
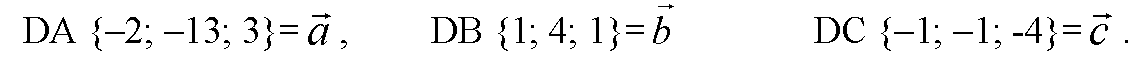
Запишем равенство
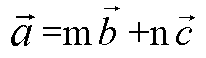
В координатах (условие компланарности):
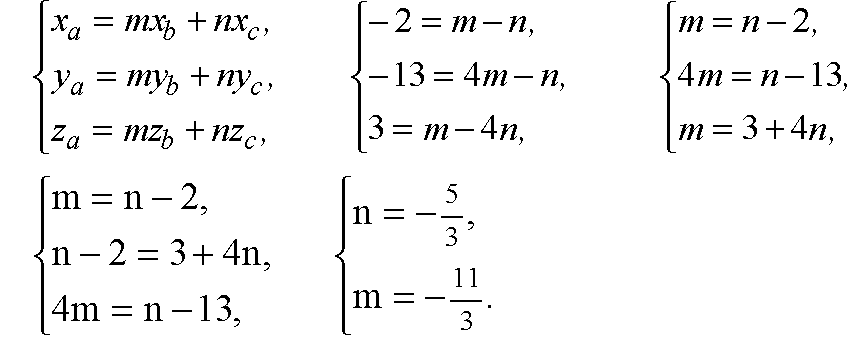
Получаем равенство:
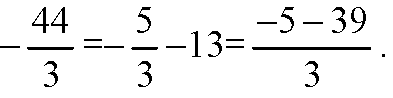
Признак компланарности векторов выполняется
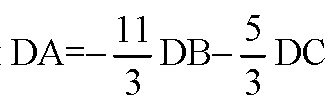
По определению векторы DA, DB и DC компланарны. Следовательно, точки А, В, С и D лежат в одной плоскости. б) Определим координаты предполагаемых векторов:
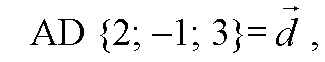
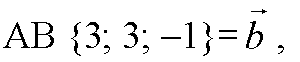
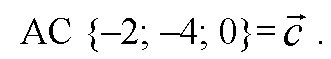
Признак компланарности векторов в координатах:
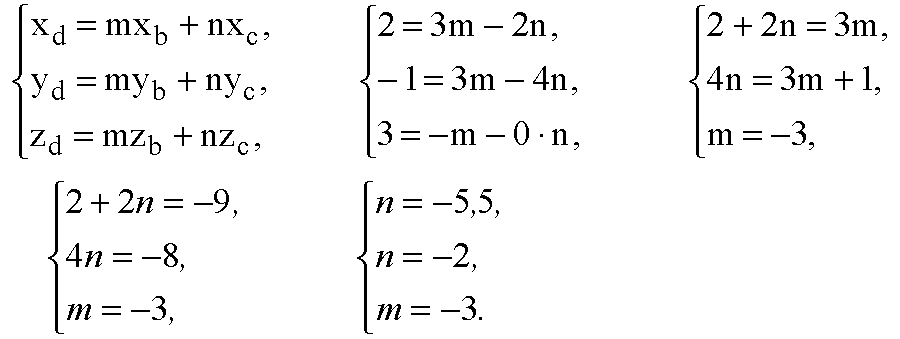
Система не имеет решений, следовательно, условие компланарности векторов не исполняется, точки А, В, С и D не лежат в одной плоскости. в) Рассмотрим векторы:
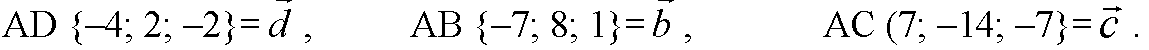
Признак компланарности векторов
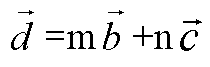
В координатах x, y, z:
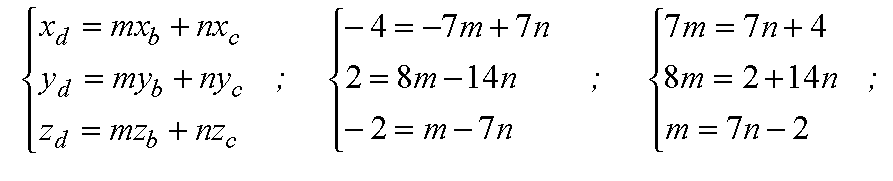
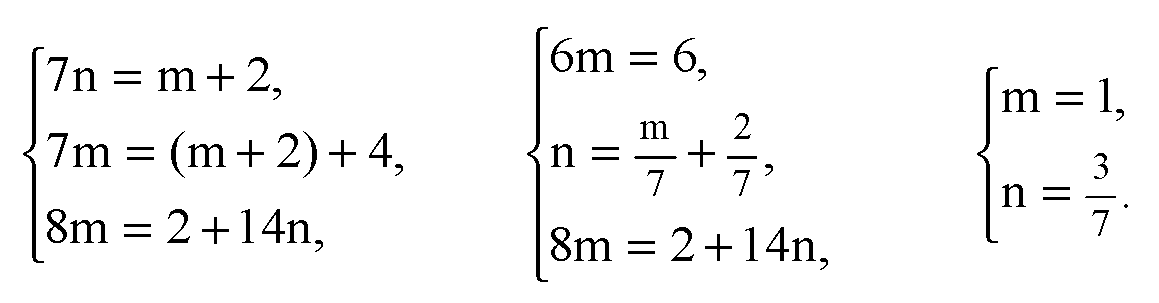
Подставляя эти значения в третье уравнение, получаем равенство:
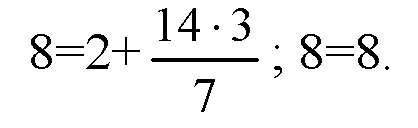
Следовательно, векторы компланарны при
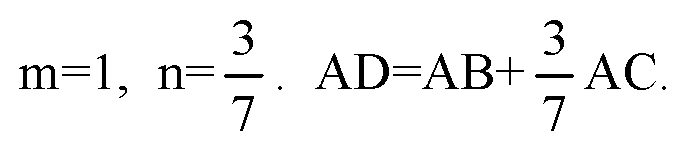
При этом все три вектора отложены из одной точки, значит, точки А, В, С и D лежат в одной плоскости.
