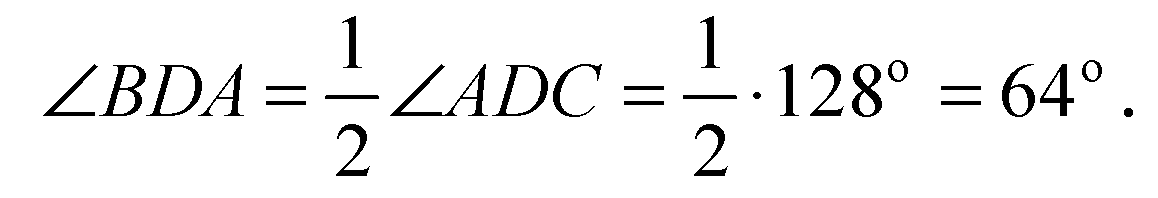Глава I Параллельность прямых и плоскостей. §2 Взаимное расположение прямых в пространстве. Угол между двумя прямыми. → номер 46
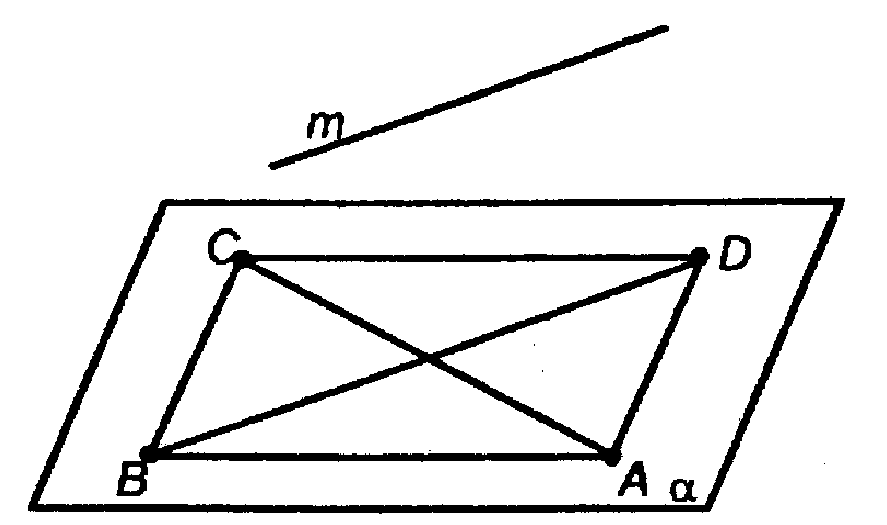
1.
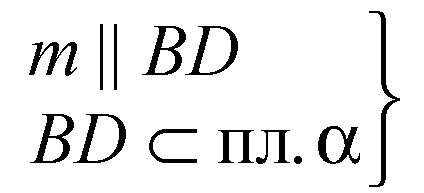
Из теоремы I
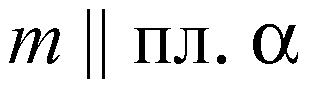
2. АС пересекает BD, то есть m и АС скрещиваются.
3. AD пересекает BD, то есть m и AD скрещиваются.
4. Угол между m и АС — равен углу между BD, параллельной m и АС.
Угол между m и АС равен 90о в силу перпендикулярности диагоналей ромба.
5. Угол между m и AD — равен углу между BD, параллельной m и AD.
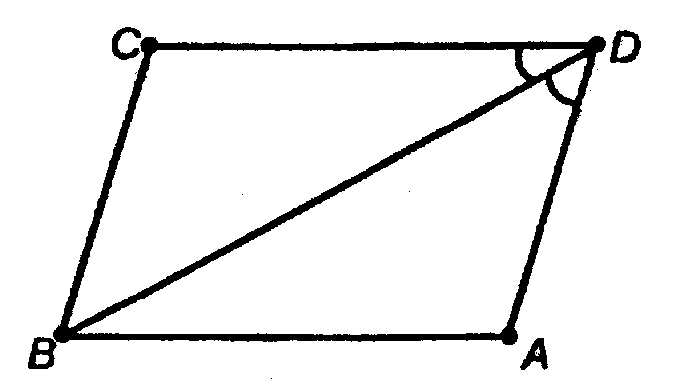
BD — биссектриса (т. к. ABCD — ромб).