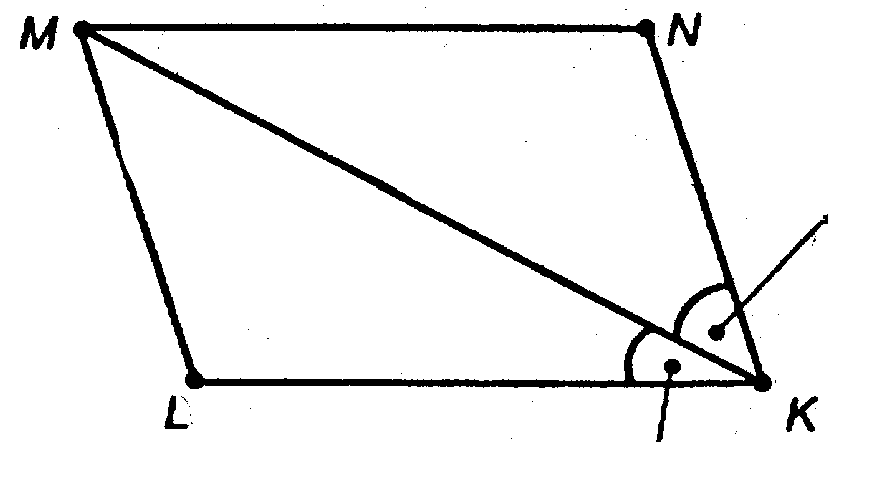
Глава I Параллельность прямых и плоскостей. §2 Взаимное расположение прямых в пространстве. Угол между двумя прямыми. → номер 47
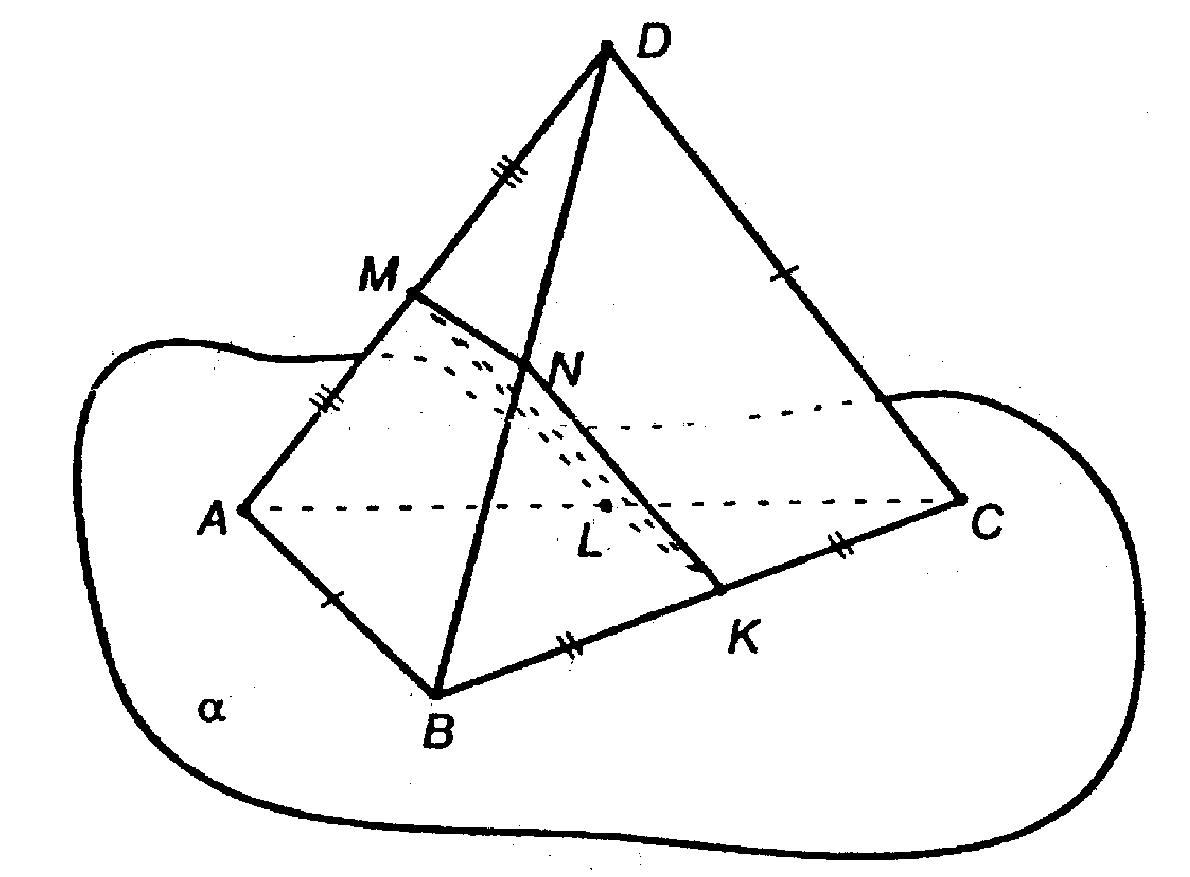
Соединим точки D и B, А и С.
Проведем в пл. α (или пл. АВС)
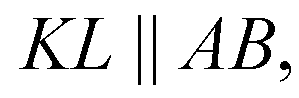
В пл.
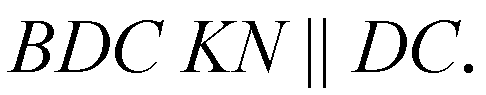
Соединив точки N и М, точки L и М, рассмотрим MNKL.
В
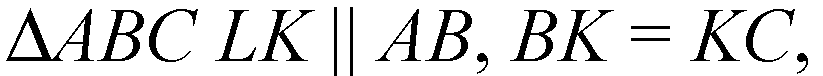
Поэтому LK — средняя линия в ΔАВС;
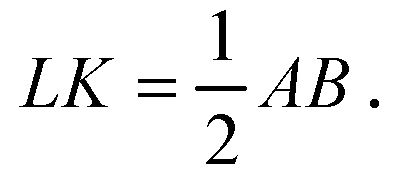
В ΔBDC KN || DC, K — середина ВС, поэтому KN — средняя линия в ΔBDC.
В ΔADB т. М — середина AD, т. N — середина BD, поэтому MN — средняя линия в ΔADB;
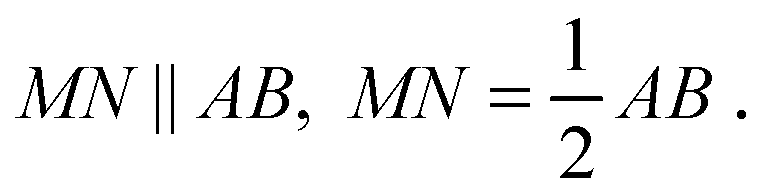
В
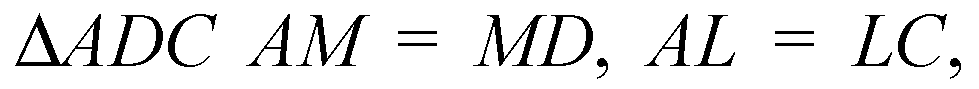
Поэтому ML — средняя линия в
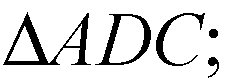
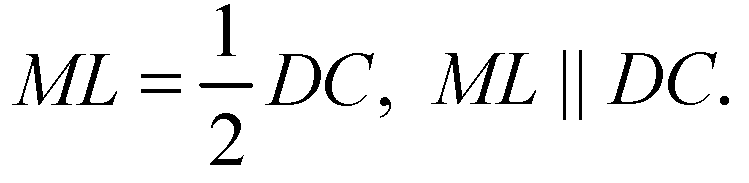
Значит,
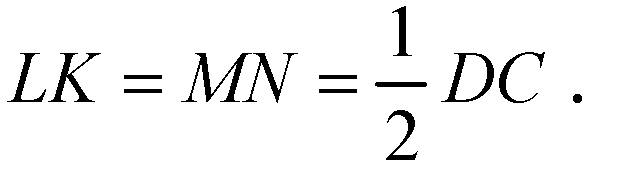
Из условия,
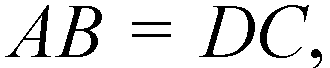
Значит,
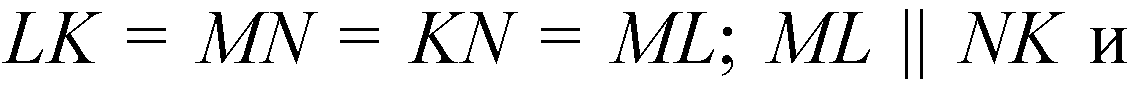
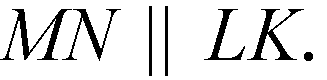
4-угольник MNKL — ромб, MK — диагональ, а в ромбе и биссектриса. Но углы NKM и LKM — искомые.