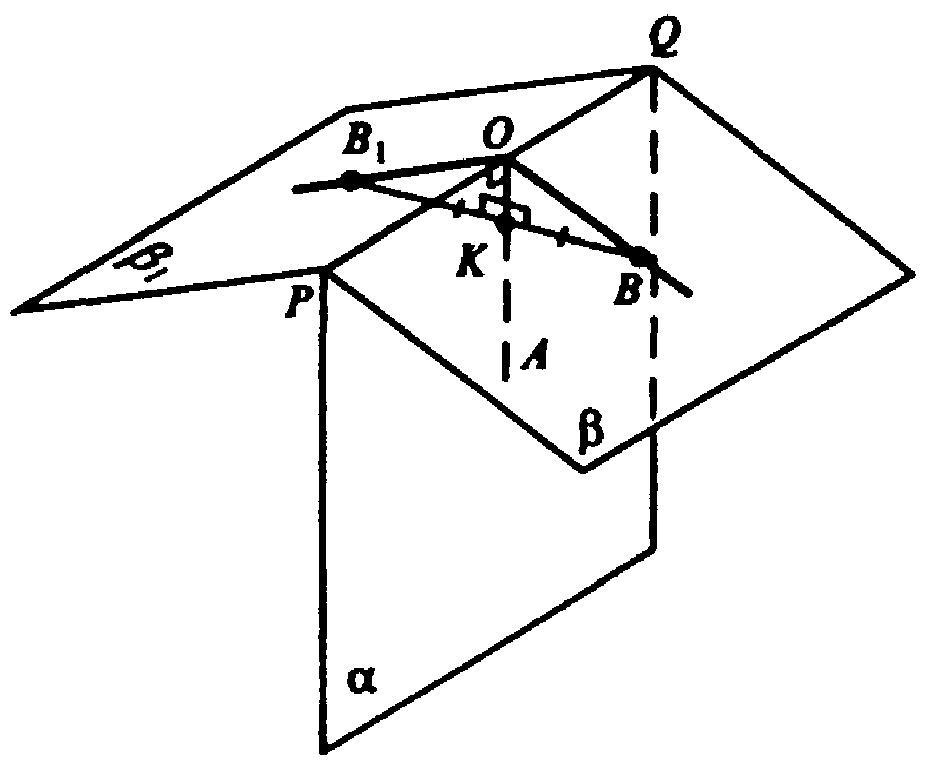
Дополнительные задачи к главе V Метод координат в пространстве → номер 519 519. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β1. Докажите, что если плоскость β образует с плоскостью α угол φ, то и плоскость β1 образует с плоскостью α угол φ.
(смотри рисунок).
Возьмем на ребре двугранного угла PQ точку О; проведем прямую
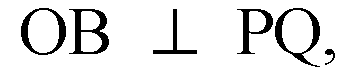
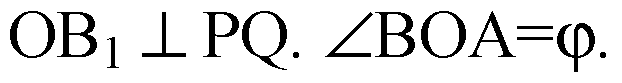
При зеркальной симметрии
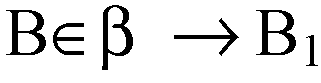
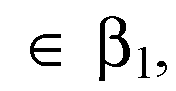
При этом
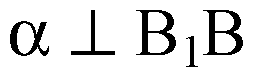
И проходит через
Середину отрезка B1B:
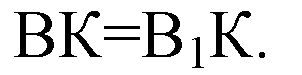
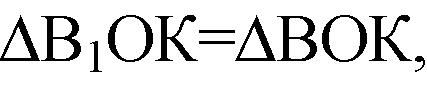
Кроме того они прямоугольные (OK ⊥ PQ, OK — общий катет, B1К=KB).
Тогда,
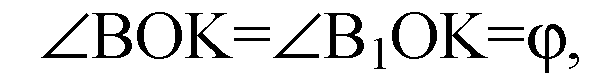
Т. к.
Линейные меры двугранных углов равны, то и соответствующие двугранные углы между плоскостями α и β, α и β1 тоже равны.
