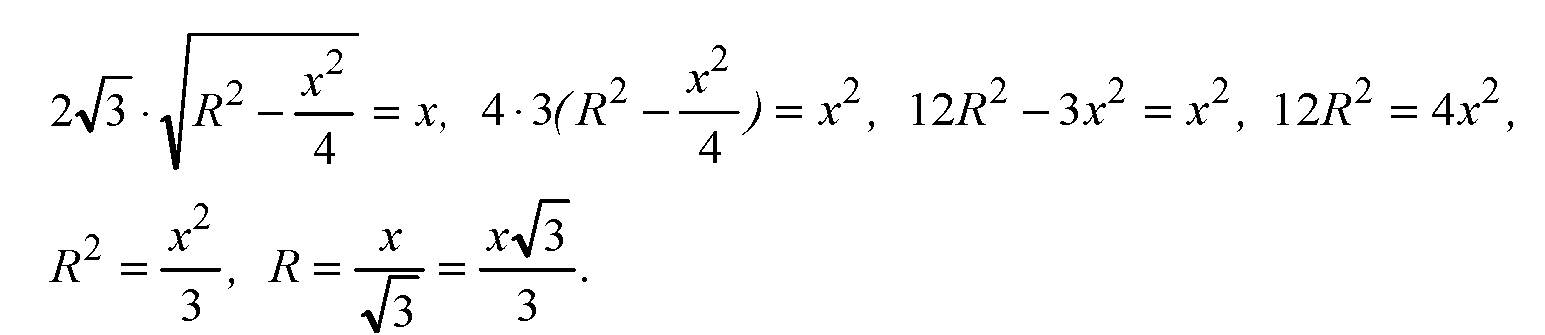Глава VI. Цилиндр, конус и шар. Дополнительные задачи → номер 602 602. Вершины А и В прямоугольника ABCD лежат на окружности одного из оснований цилиндра, а вершины С и D — на окружности другого основания. Вычислите радиус цилиндра, если его образующая равна а, АВ=а, а угол между прямой ВС и плоскостью основания равен 60°.
ABCD — прямоугольник.
Через центры оснований проведем диаметры, перпендикулярные к сторонам АВ и DC. О1М ⊥ АВ, ON ⊥ DC.
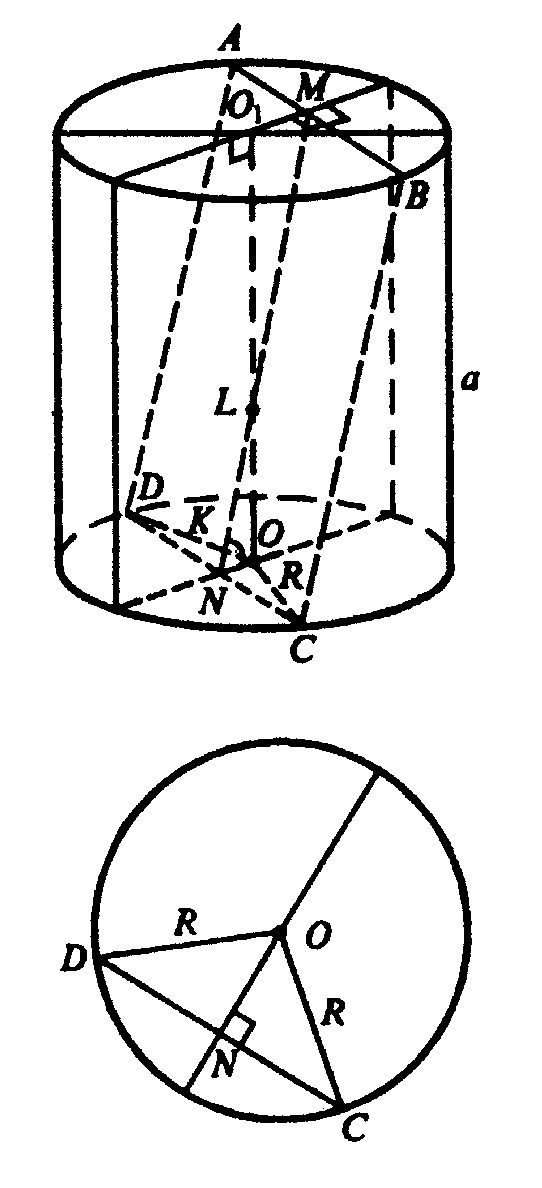
Из планиметрии известно, что диаметр, перпендикулярный к хорде, делит хорду пополам, следовательно, точка N и точка М — середины DC и АВ соответственно. Отрезок MN параллелен сторонам AD и ВС,
∠MNO = 60° — угол между прямой ВС (или ей параллельной MN) и плоскостью основания.
Пусть R — радиус основания цилиндра.
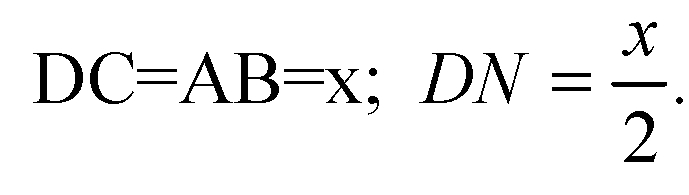
Из ΔDNO получим:
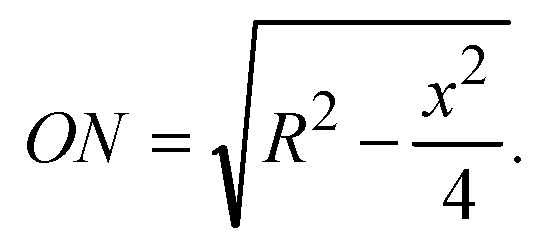
Из прямоугольного треугольника LON:
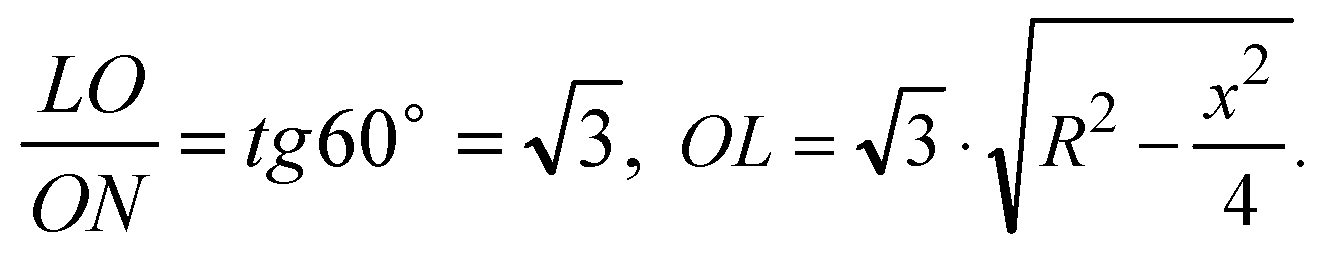
Рассмотрим плоскость верхнего основания
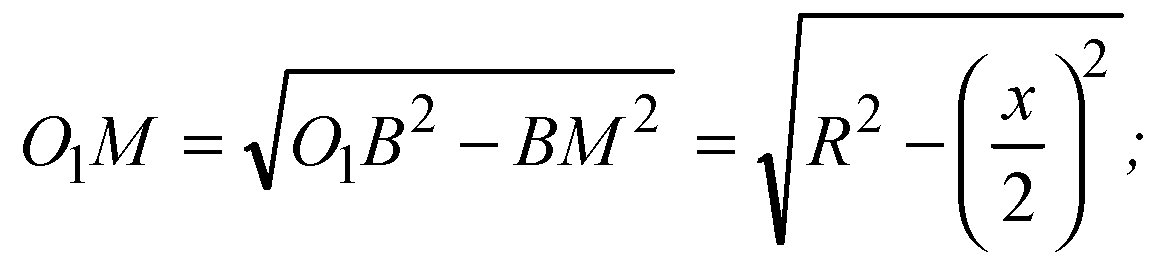
Следовательно, O1M = ON.
Значит ΔO1LM=ΔOLN, отсюда OL=O1L.
O1L+LO=O1O=х (высота цилиндра равна его образующей).