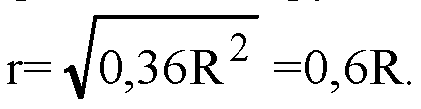Глава VI. Цилиндр, конус и шар. Дополнительные задачи → номер 625
Введем систему координат, согласно рисунку.
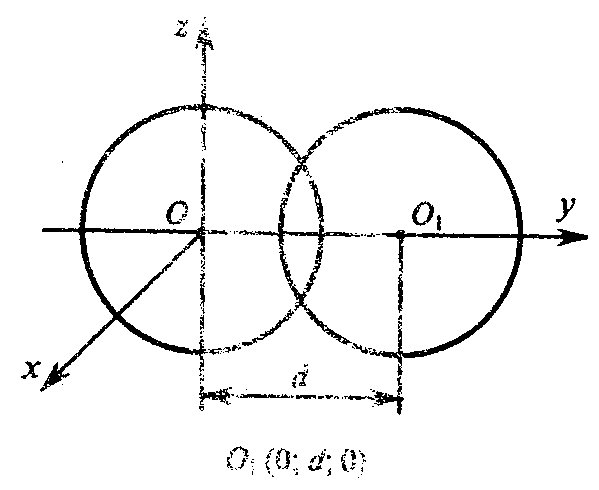
Уравнение сферы с центром в точке О:
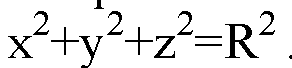
Уравнение сферы с центром в точке O1.
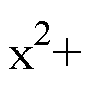
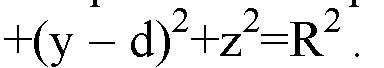
Решение системы:
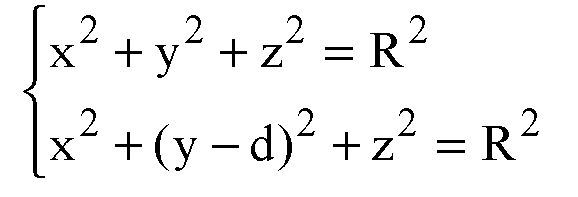
Дает ответ на вопрос задачи.
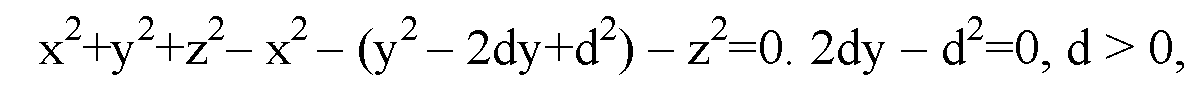
Поэтому
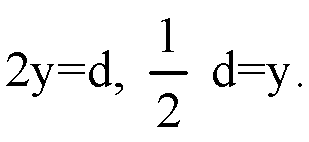
Согласно условию задачи
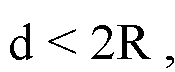
Тогда,
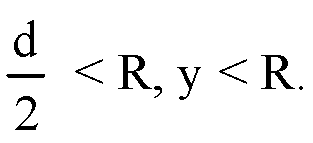
Значит, есть некоторая плоскость, которая перпендикулярна оси ординат (а значит, параллельная плоскости Охz) и пересекает сферу, а при пересечении сферы плоскостью в сечении получим окружность. Утверждение а) доказано.
Подставим значение
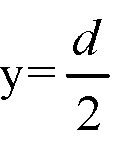
В уравнение сферы
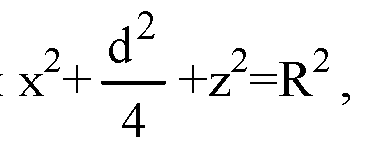
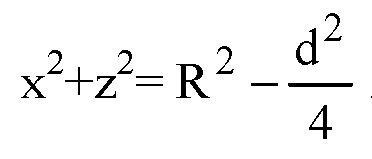
Если d=1,6R, то
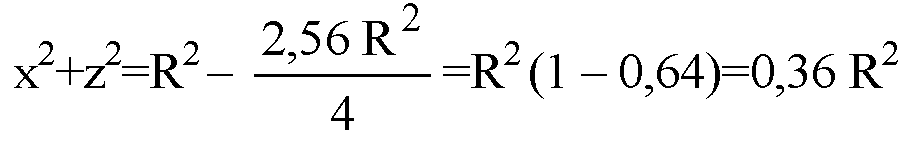
Это уравнение окружности в плоскости, параллельной плоскости Охz, ее радиус