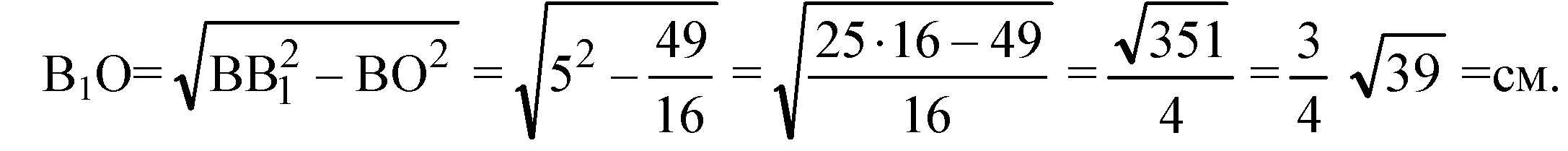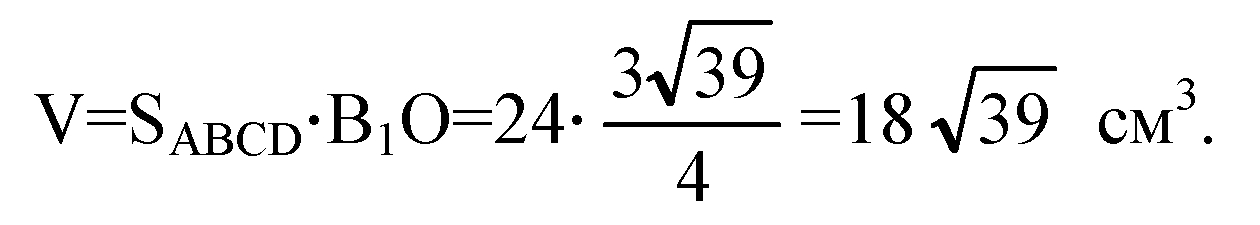Глава VII. Объемы тел. § 3. Объём наклонной призмы, пирамиды и конуса → номер 681
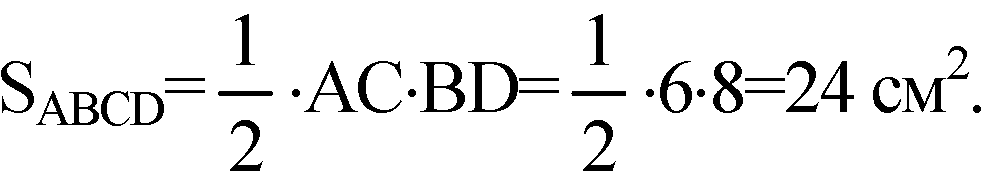
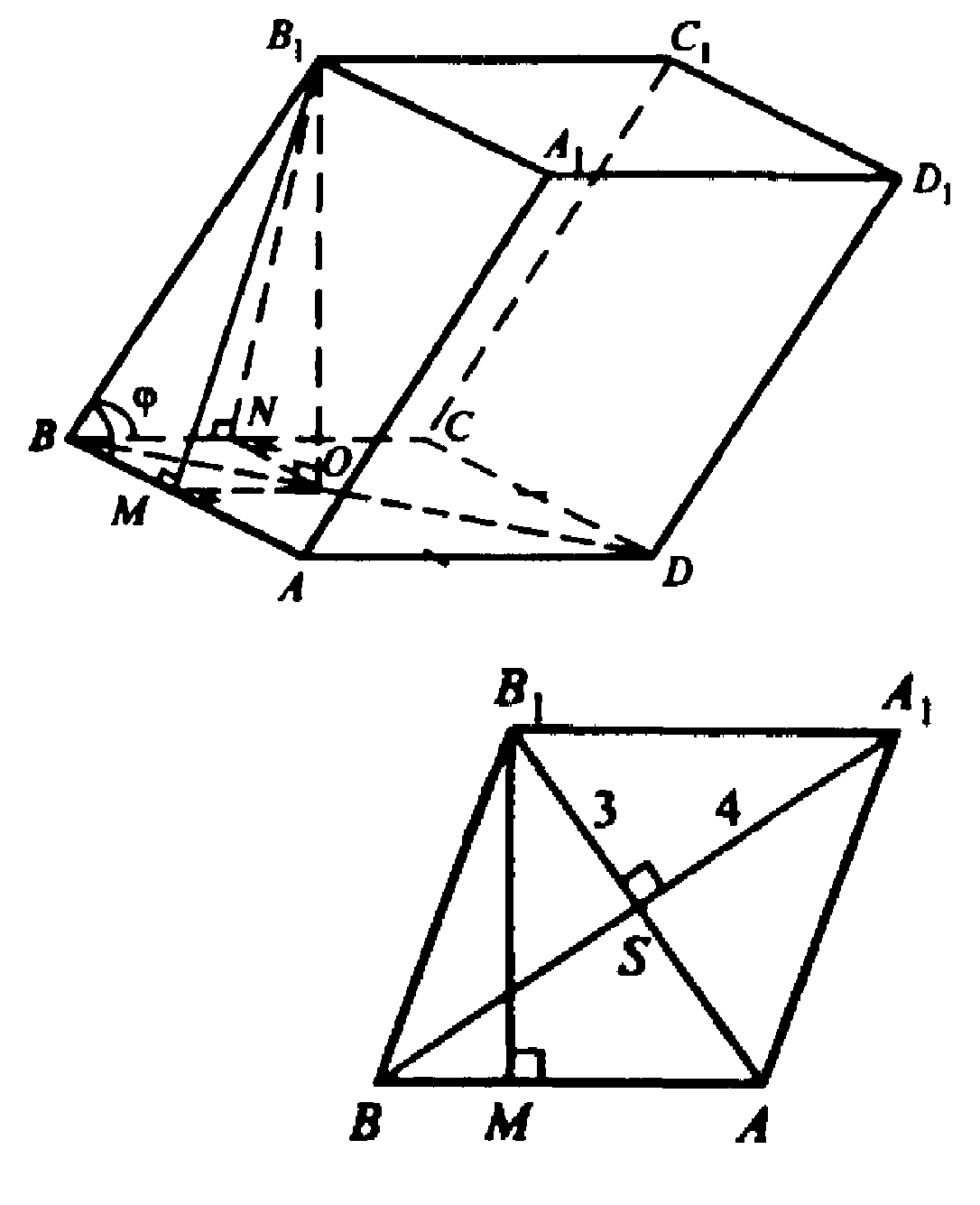
Вычислим высоту параллелепипеда. Боковое ребро ВВ1 составляет со смежными сторонами основания равные углы; обозначим
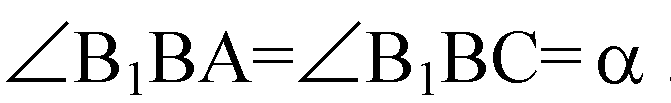
Проведем В1М⊥ВА и B1N⊥BС.
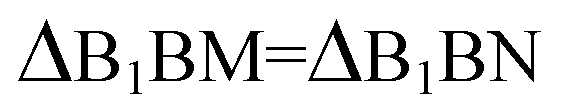
(по гипотенузе и острому углу).
Тогда, В1М=В1N. Проведем В1О ⊥ плоскости ABCD, отрезки ON и ОМ. ON=OM (как проекции равных отрезков). Точка О равноудалена от сторон ромба ВС и ВА, то есть она лежит на биссектрисе угла АВС, а в ромбе биссектрисой угла служит диагональ ромба, значит, точка О лежит на диагонали ромба DB. В1О — высота параллелепипеда.
По свойству диагоналей ромба ∠ASB=90° и B1S=3, A1S=4. Следовательно, сторона ромба
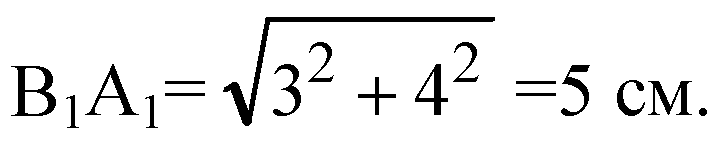
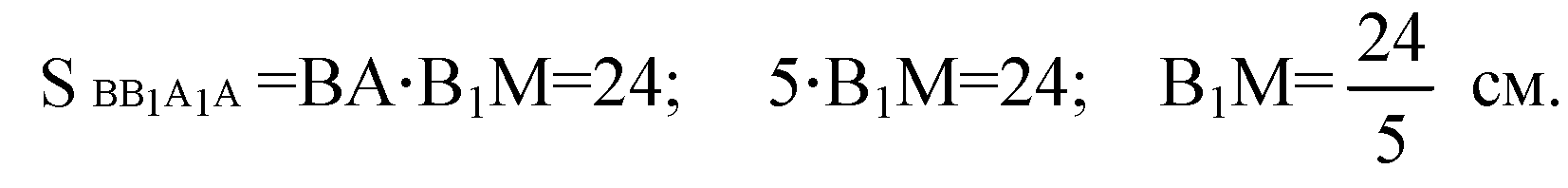
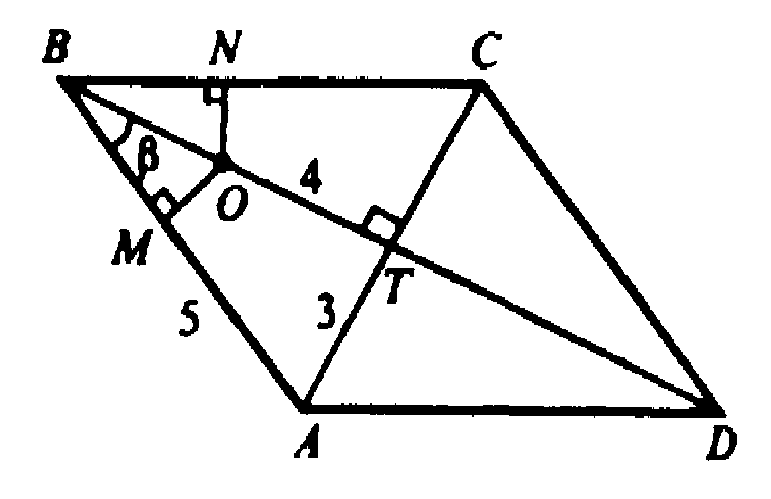
Из прямоугольного треугольника ΔВ1МВ:
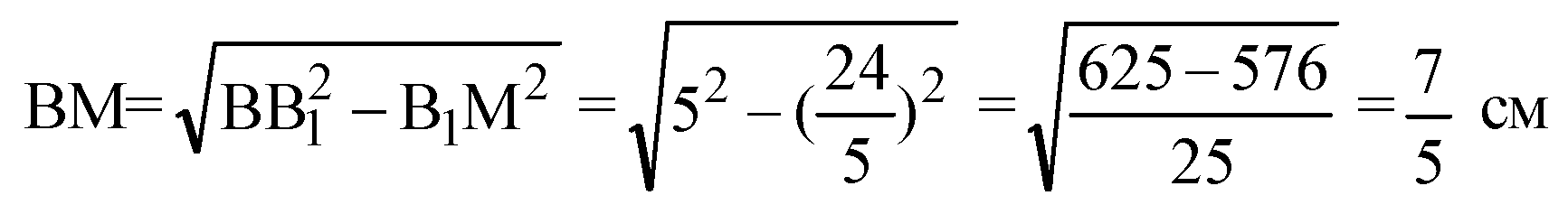
Из ΔABT:
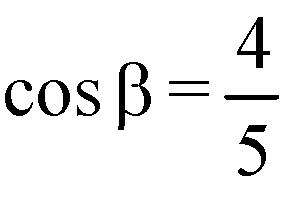
Из ΔМОВ:
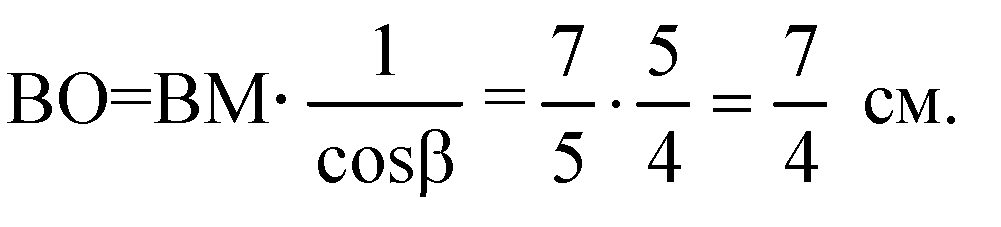
Из прямоугольного треугольника ΔВ1ОВ: