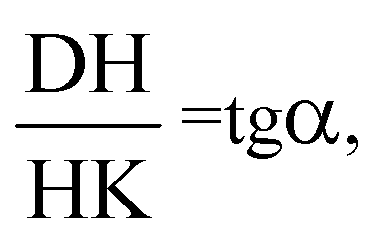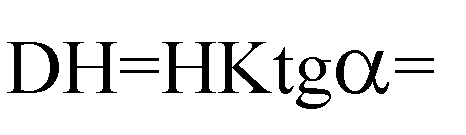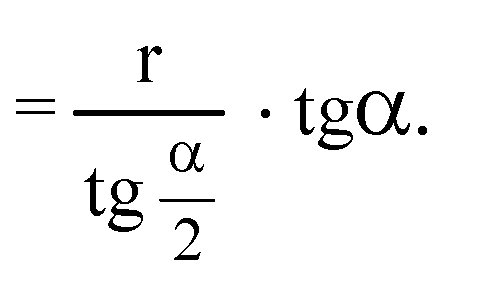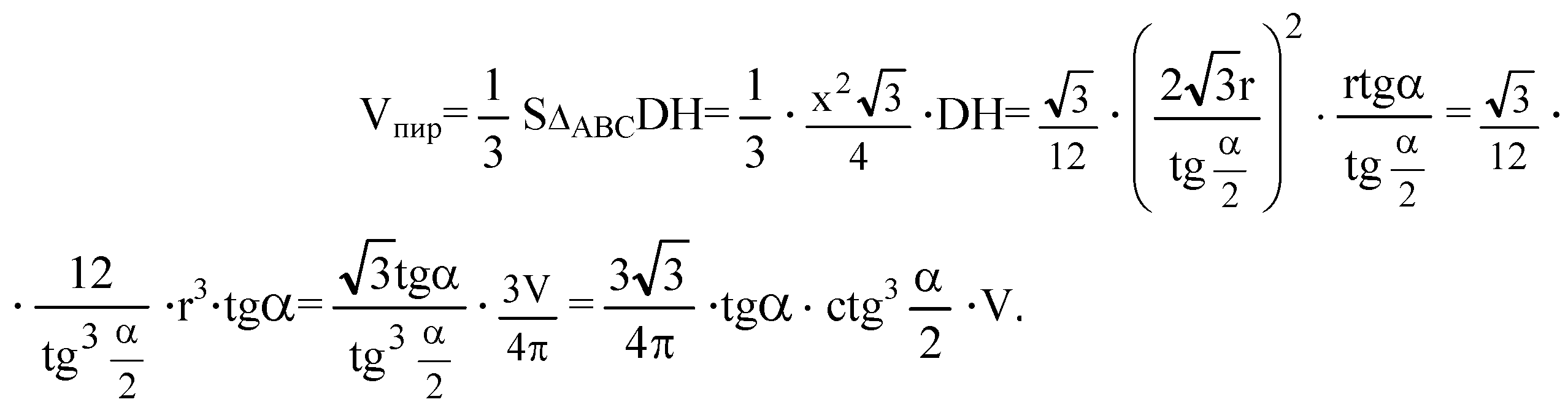Разные задачи на многогранники, цилиндр, конус и шар → номер 754
Через основание высоты DH построим АК⊥ВС, отрезок DK. По теореме о трех перпендикулярах DK перпендикулярно BC.
Центр вписанного шара находится на высоте пирамиды в точке О; ОН и OF — радиусы, равные r. По условию задачи
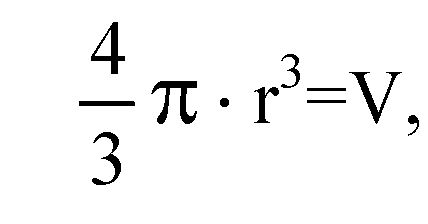
Поэтому
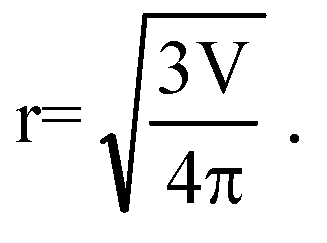
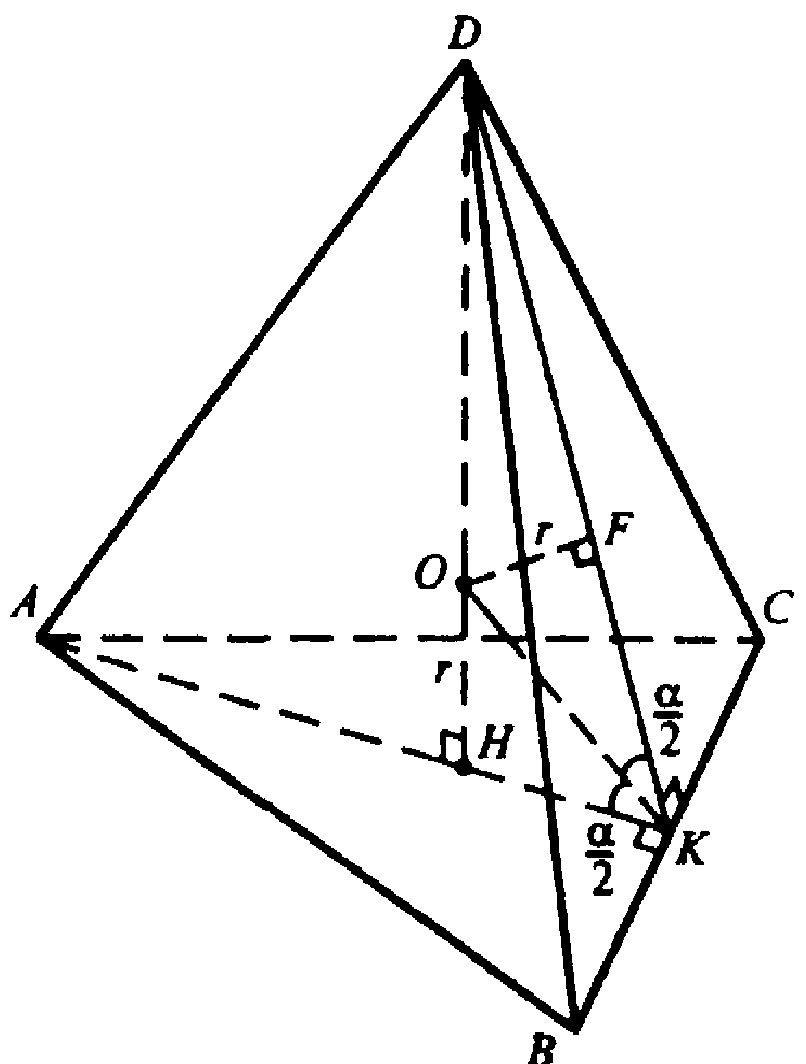
Т. к. АК⊥ВС и DK⊥ВС, то ∠AKD — линейный угол двугранного угла при основании пирамиды.
∠AKD=α. ОК — биссектриса ∠DKA. Из равенства (ΔOHK=ΔOFK),

Обозначим сторону основания пирамиды за а. В равностороннем треугольнике АВС — НК это радиус вписанной окружности и
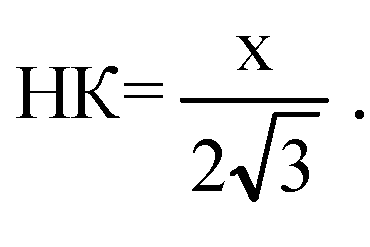
Из прямоугольного треугольника ОНК:
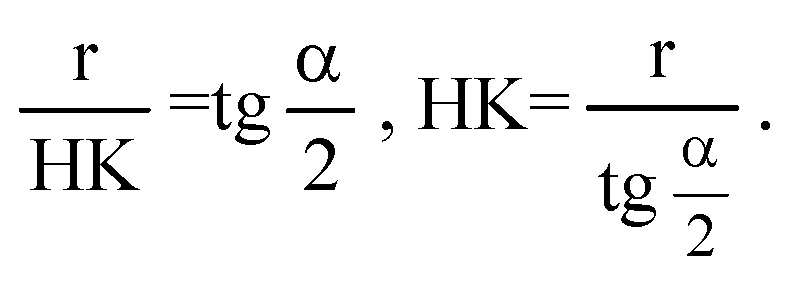
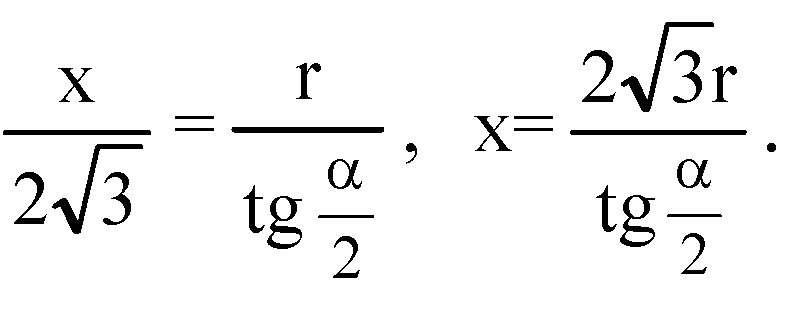
В треугольнике DHK: