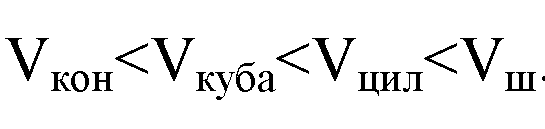Разные задачи на многогранники, цилиндр, конус и шар → номер 762
Пусть ребро куба равно а. Площадь поверхности куба равна 6а2.
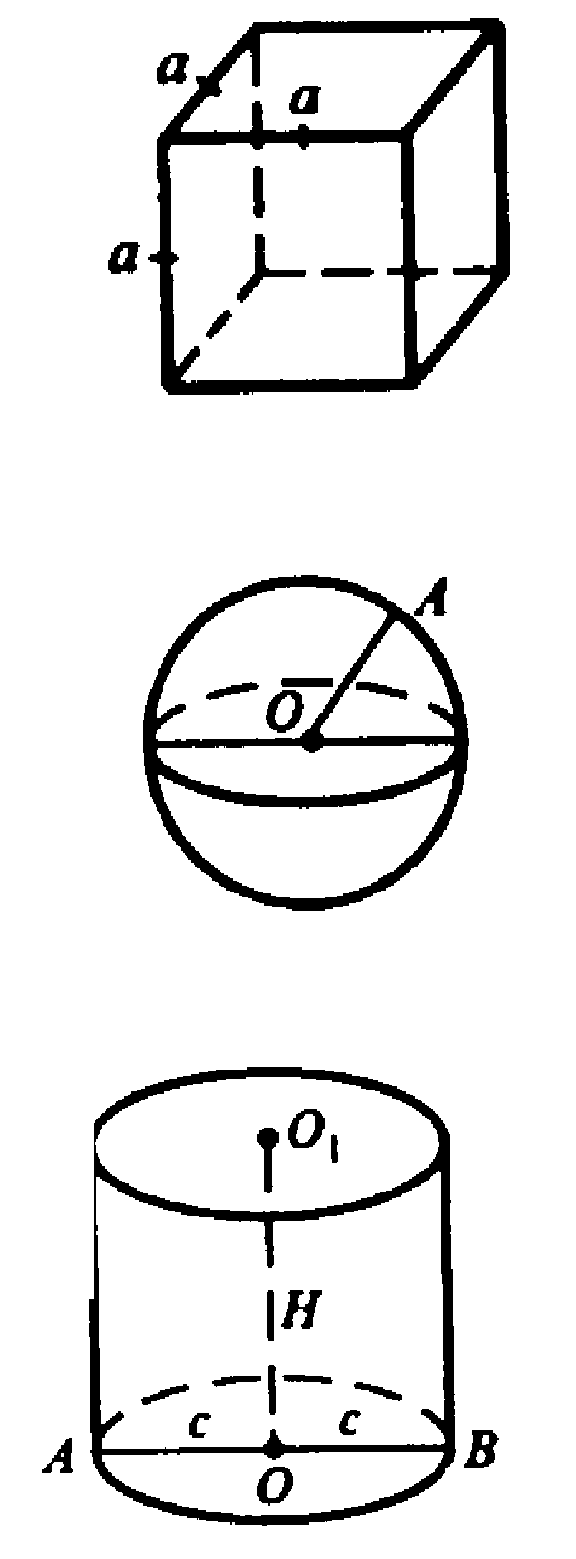
Пусть радиус шара ОА=b. Площадь поверхности шара
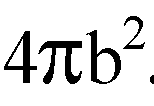
Пусть радиус основания цилиндра равен с, тогда АВ=Н=2с.
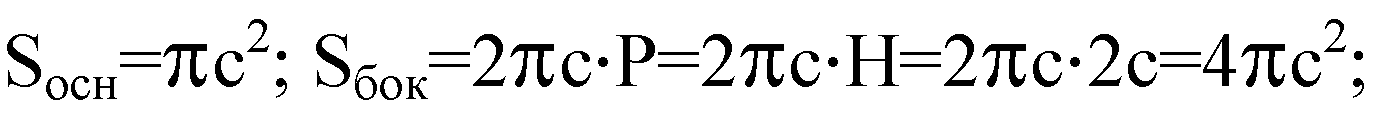
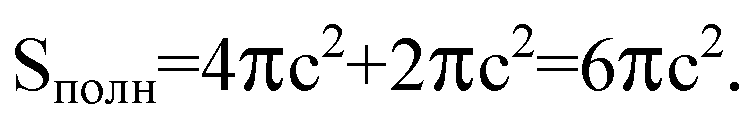
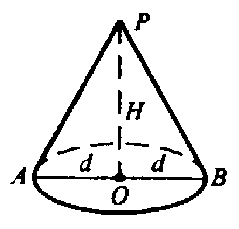
Пусть радиус основания конуса равен d, тогда РО=Н=2d.
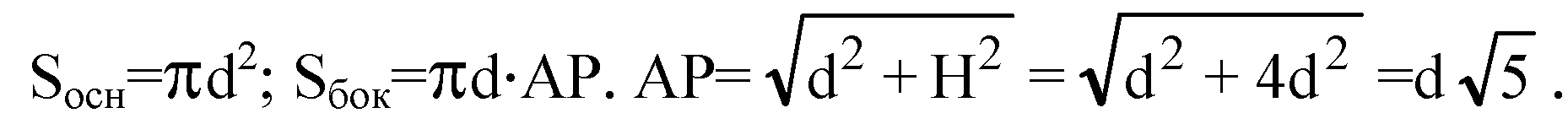
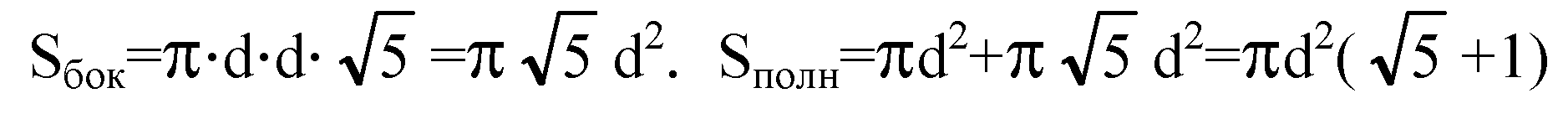
(из
Условия).
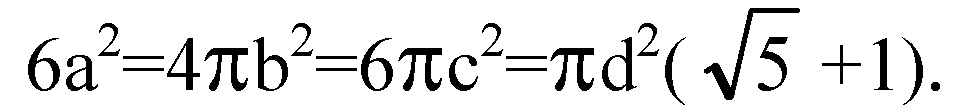
Выразим a, с и d через b.
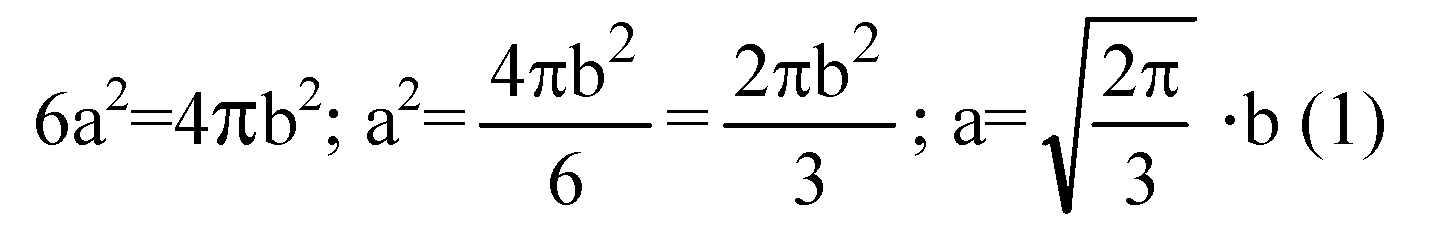
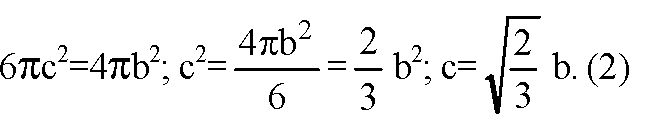
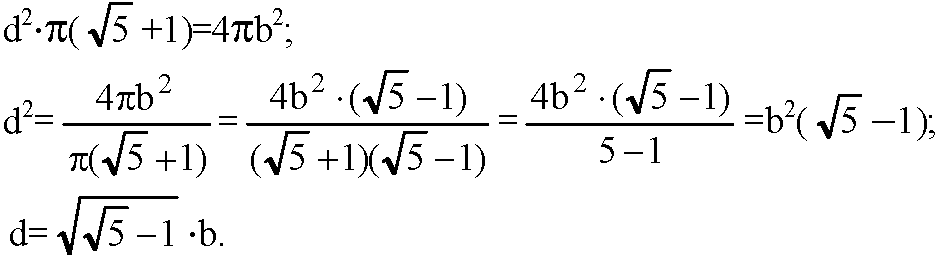
Объем куба равен а3;
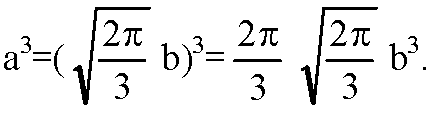
Объем шара равен
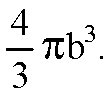
Объем цилиндра равен
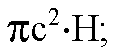
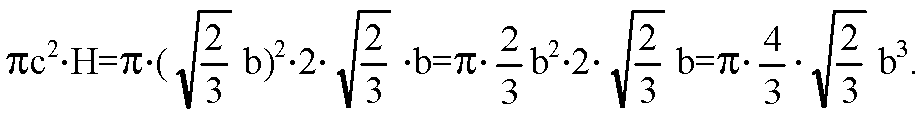
Объем конуса равен
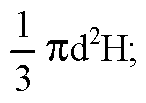
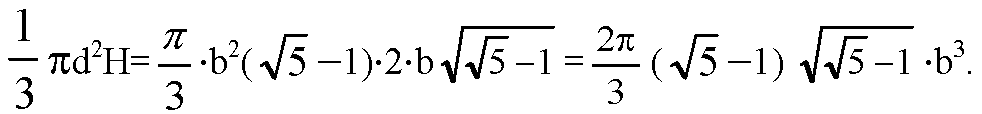
Сравним объемы тел. Т. к. все они выражены через радиус шара b, то остается сравнивать коэффициенты при b3.
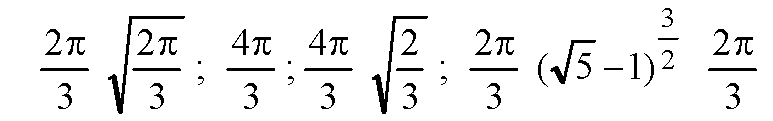
— общий множитель. Следовательно, остаются числа:
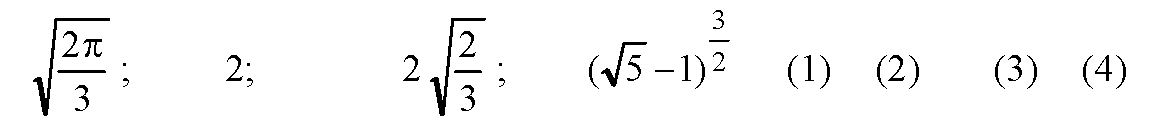
Сравним числа (1) и (2).
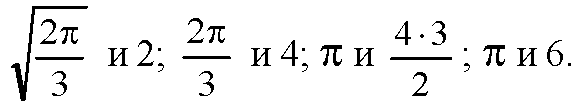
Т. к. π<6, то
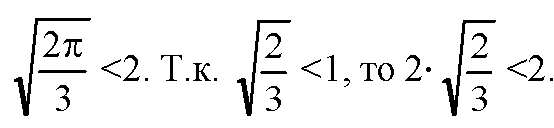
Сравним теперь (1) и (3).
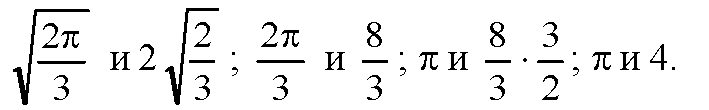
Т. к.
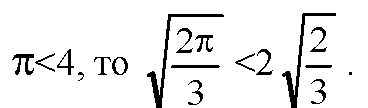
Таким образом, установлено, что
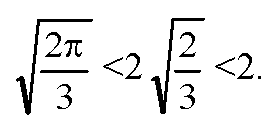
Сравним теперь (4) и (1).
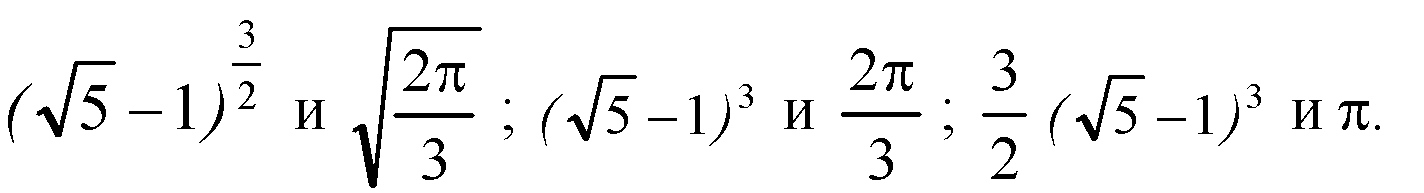
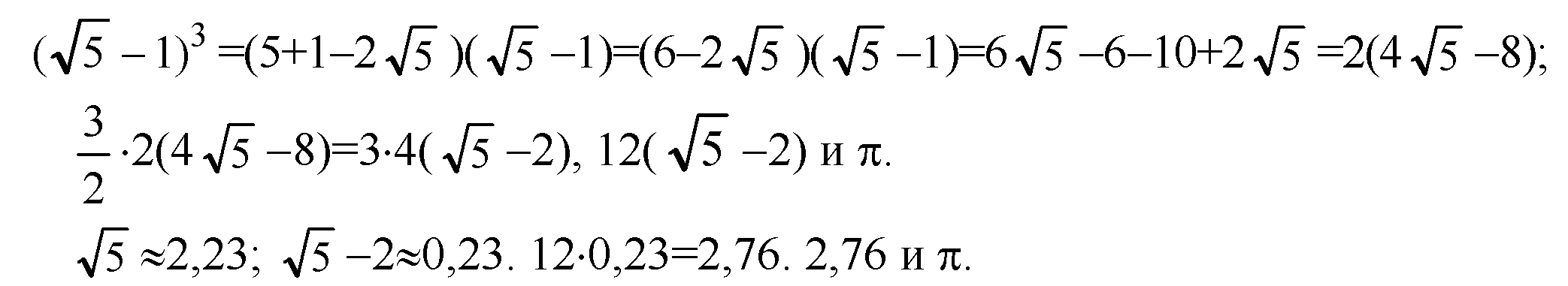
Т. к.
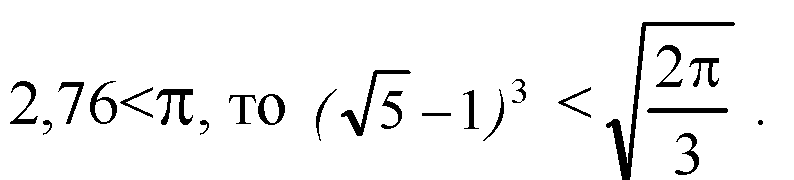
Таким образом, числа расположены в следующем порядке:
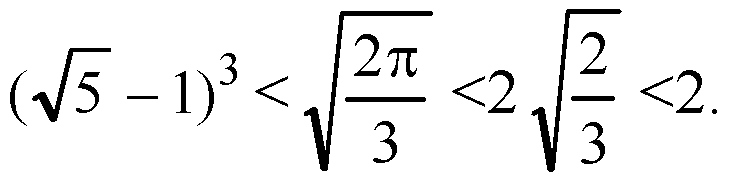
Им соответствует объемы тел: