Задачи повышенной трудности → номер 792
Пусть высоты АА1, ВВ1, СС1, DD1 тетраэдра ABCD пересекаются в точке H; α — плоскость АВН,
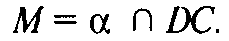
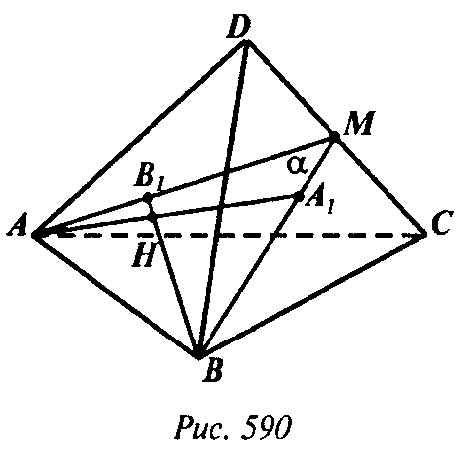
Т. к.
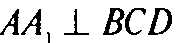
И
То
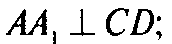
Аналогично
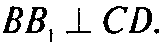
Т. к.
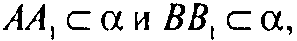
То
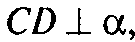
Но
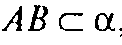
Следовательно,
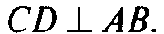
Аналогично доказывается, что
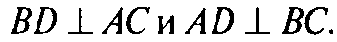
Обратно, пусть
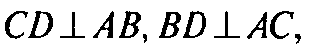
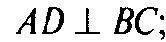
α — плоскость АВА1.
Так как
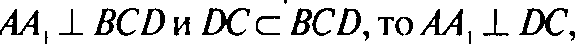
А поскольку и по ус
Ловию
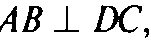
То
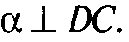
Так как
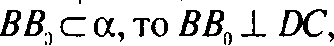
Но вместе с
Тем
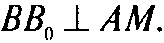
Поскольку
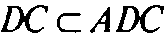
И
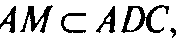
То
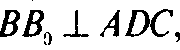
То
Есть ВВ0 совпадает с высотой ВВ1 тетраэдра.
Таким образом, высоты АA1 и ВВ1 тетраэдра пересекаются в точке H; аналогично и остальные высоты тетраэдра попарно пересекаются. Их точки пересечения совпадают, так как в противном случае все высоты тетраэдра лежали бы в одной плоскости.
