795. Из точки сферы проведены три попарно перпендикулярные хорды. Докажите, что сумма их квадратов не зависит от положения этих хорд

Задачи повышенной трудности → номер 795

Пусть О — центр сферы, SA = а, SB = b, SC = с — данные хорды, α — плоскость SAB, ω — сечение сферы этой плоскостью.

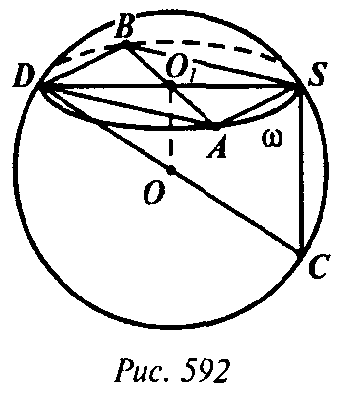
Так как ∠ASB = 90°, то АВ — диаметр для ω. Если DS — другой диаметр, то ASBD — прямоугольник и точка O1 пересечения его диагоналей — центр для ω и, следовательно, OO1 ⊥ α. Поскольку SC ⊥ SA и SC ⊥ SB, то SC ⊥ α и, значит, SC II OO1. Плоскость, проходящая через эти прямые, содержит большой круг шара. Так как ∠DSC = 90°, то DC — диаметр сферы.

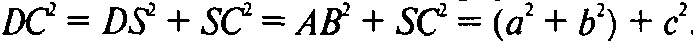
Сумма а2 + b2 + с2 равна квадрату диаметра сферы и, следовательно, не зависит от положения хорд.