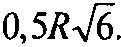Задачи повышенной трудности → номер 797
Пусть SA, SB, SC — данные касательные к сфере радиуса R с центром О. ΔASO = ΔBSO = ΔSCO как прямоугольные по гипотенузе SO и катету R, следовательно, SA = SB = SC. ΔASB = ΔBSC = ΔCSA по двум катетам, поэтому АВ = ВС = AC. Перпендикуляры, опушенные из S и О на плоскость ABC, пройдут поэтому через центр О, окружности, описанной около ΔАВС, и совпадут. Если SA = а, то из треугольника ABS: АВ = а√2.
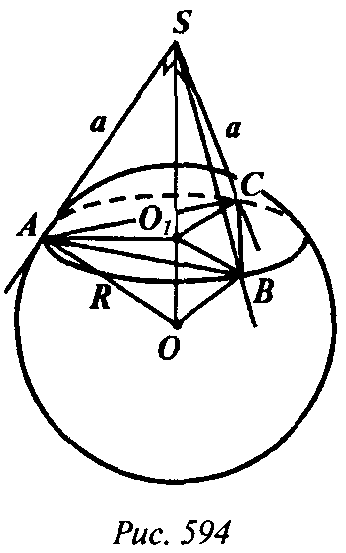
Так как O1А — радиус описанного около треугольника ABC круга, то
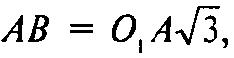
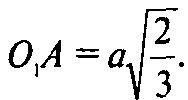
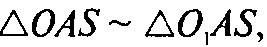
Следовательно,
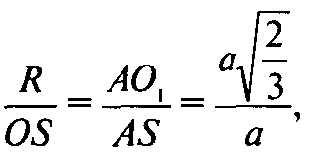
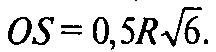
Искомое множество — сфера, центр которой совпадает с центром данной сферы, а радиус равен