Задачи повышенной трудности → номер 812
При повороте пирамиды SABCD вокруг прямой p, параллельной АВ, отрезки A0A, SM, В0В, перпендикулярные р, займут соответственно положения A0A1, SM1, B0B1 в плоскости
SA2B2.
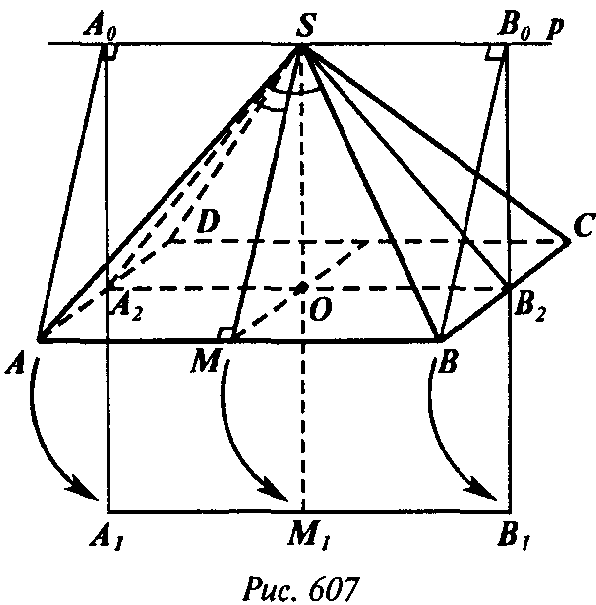
Поэтому тело, полученное при ее вращении, совпадает с телом, полученным при вращении многоугольника A1A2SB2B1. Его объем равен разности между объемом цилиндра, полученного при вращении прямоугольника A1B1B0A0, и объемами конусов, полученных при вращении равных треугольников A2A1S и B2B0S.
Из ΔASM:
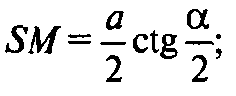
Из ΔOSM:
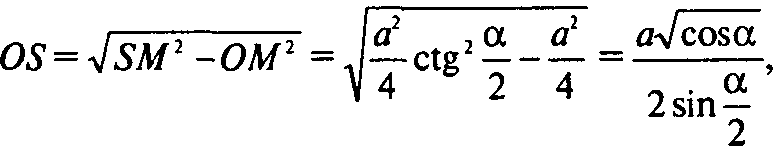
Но
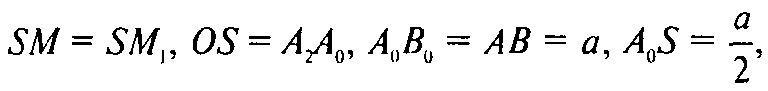
Поэтому объем тела
Вращения равен