Десять молодых людей решили отпраздновать окончание средней школы товарищеским обедом в ресторане. Когда все собрались, и первое блюдо было подано, заспорили о том, как усесться вокруг стола. Одни предлагали разместиться в алфавитном порядке, другие — по возрасту, третьи — по успеваемости, четвертые — по росту и т. д. Спор затянулся, суп успел остыть, а за стол никто не садился. Примирил всех официант, обратившийся к ним с такой речью:
— Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.
Все сели как попало. Официант продолжал:
— Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда — обещаю торжественно — я начну ежедневно угощать вас бесплатно самыми изысканными обедами.
Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами.
Однако, им не пришлось дождаться этого дня. И вовсе не потому, что официант не исполнил обещания, а потому, что число всех возможных размещений за столом чересчур велико. Оно равняется ни мало, ни много — 3628800. Такое число дней составляет, как нетрудно сосчитать, почти 10000 лет!
Вам, быть может, кажется невероятным, чтобы 10 человек могли размещаться таким большим числом различных способов. Проверьте расчет сами.
Раньше всего надо научиться определять число перестановок. Для простоты начнем вычисление с небольшого числа предметов — с трех. Назовем их А, Б и В.
Мы желаем узнать, сколькими способами возможно переставлять их один на место другого. Рассуждаем так.
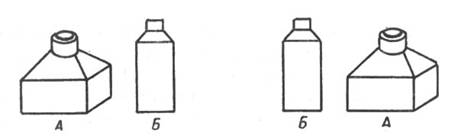
Рис. 55. Две вещи можно разместить только двумя способами
Если отложить пока в сторону вещь В, то остальные две можно разместить только двумя способами.
Теперь будем присоединять вещь В к каждой из этих пар. Мы можем сделать это трояко: можем
- Поместить В позади пары,
- Поместить В впереди пары,
- Поместить В между обеими вещами.
Других положений для вещи В, кроме этих трех, очевидно, быть не может. А так как у нас две пары, АБ и БА, то всех способов разместить вещи наберется
2 х 3 = 6.
Способы эти показаны на рис. 56.
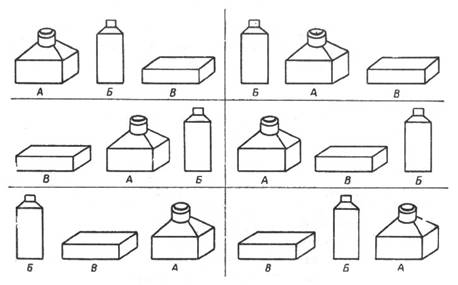
Рис. 56. Три вещи можно разместить шестью способами
Пойдем дальше — сделаем расчет для 4 вещей.
Пусть у нас 4 вещи: А, Б, В и Г. Опять отложим пока в сторону одну вещь, например Г, а с остальными тремя сделаем все возможные перестановки. Мы знаем уже, что число этих перестановок — 6. Сколькими же способами можно присоединить четвертую вещь Г к каждой из 6 троек? Очевидно, четырьмя: можно
- Поместить Г позади тройки;
- Поместить Г впереди тройки:
- Поместить Г между 1-й и 2-й вещью;
- Поместить Г между 2-й и 3-й вещью.
Всего получим, следовательно,
6 x 4 = 24 перестановки;
А так как 6 = 2 x 3, а 2 = 1 x 2, то число всех перестановок можно представить в виде произведения:
1 x 2 x 3 x 4 = 24.
Рассуждая таким же образом и в случае 5 предметов, узнаем, что для них число перестановок равно
1 x 2 x 3 x 4 x 5 = 120.
Для 6 предметов:
1 x 2 x 3 x 4 x 5 x 6 = 720 и т. д.
Обратимся теперь к случаю с 10 обедающими. Число возможных здесь перестановок определится, если дать себе труд вычислить произведение
1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10.
Тогда и получится указанное выше число
3628800.
Расчет был бы сложнее, если бы среди 10 обедающих было 5 девушек, и они желали бы сидеть за столом непременно так, чтобы чередоваться с юношами. Хотя число возможных перемещений здесь гораздо меньше, вычислить его несколько труднее.
Пусть сядет за стол — безразлично как — один из юношей. Остальные четверо могут разместиться, оставляя между собою пустые стулья для девушек, 1 x 2 x 3 x 4 = 24 различными способами. Так как всех стульев 10, то первый юноша может сесть 10 способами; значит число всех возможных размещений для молодых людей 10X X 24=240.
Сколькими же способами могут сесть на пустые стулья между юношами 5 девушек? Очевидно, 1x2x3x4x5 = 120 способами. Сочетая каждое из 240 положений юношей с каждым из 120 положений девушек, получаем число всех возможных размещений:
240 x 120 = 28800.
Число это во много раз меньше предыдущего и потребовало бы всего 79 лет (без малого). Доживи молодые посетители ресторана до столетнего возраста, они могли бы дождаться бесплатного обеда, если не от самого официанта, то от его наследников.
Умея подсчитывать перестановки, мы можем определить теперь, сколько различных расположений шашек возможно в коробке игры в 15*. Другими словами, мы можем подсчитать число всех задач, какие способна предложить нам эта игра. Легко понять, что подсчет сводится к определению числа перестановок из 15 предметов. Мы знаем уже, что для этого нужно перемножить
1 х 2 х 3 х 4 х... х 14 х 15.
Вычисление дает итог:
1307674365000,
Т. е. больше триллиона.
* (При этом свободная клетка должна всегда оставаться в правом нижнем углу.)
Из этого огромного числа задач половина неразрешима. Существует, значит, свыше 600 миллиардов неразрешимых положений в этой игре. Отсюда понятна отчасти та эпидемия увлечения игрой в 15, которая охватила людей, не подозревавших о существовании такого огромного числа неразрешимых случаев.
Заметим еще, что если бы мыслимо было ежесекундно давать шашкам новое положение, то, чтобы перепробовать все возможные расположения, потребовалось бы, при непрерывной работе круглые сутки, свыше 40000 лет.
Заканчивая нашу беседу о числе перестановок, решим такую задачу из школьной жизни.
В классе 25 учеников. Сколькими способами можно рассадить их по партам?
Путь решения этой задачи — для тех, кто усвоил себе все сказанное раньше, — весьма не сложен: нужно перемножить 25 таких чисел:
1 х 2 х 3 х 4 х 5 х 6 х... х 23 х 24 х 25.
Математика указывает способы сокращать многие вычисления, но облегчать выкладки, подобные сейчас приведенной, она не умеет. Не существует никакого иного способа выполнить точно это вычисление, как добросовестно перемножить все эти числа*. Только удачная группировка множителей позволит несколько сократить время вычисления. Результат получается огромный, из 26 цифр — число, величину которого наше воображение не в силах себе представить.
* (Впрочем, приближенно это вычисление может быть выполнено сравнительно несложно, В математике часто встречается необходимость вычислить произведение всех целых чисел от 1 до некоторого числа n. Это произведение обозначают символом n! и называют n-факториал. Например, выписанное выше произведение коротко обозначается как 25!. В XVIII веке английский математик Стирлинг установил формулу, позволяющую приближенно вычислять факториалы. Эта формула имеет вид
Где π = 3,141…, e = 2,718… — некоторые числа, играющие важную роль в разных вопросах математики. Пользуясь таблицами логарифмов, по формуле Стирлинга легко получить:
)
Вот оно:
15511210043330985984000000.
Из всех чисел, какие встречались нам до сих пор, — это, конечно, самое крупное, и ему больше всех прочих принадлежит право называться числом-великаном. Число мельчайших капель во всех океанах и морях земного шара скромно по сравнению с этим исполинским числом.
