В столовой дома отдыха зашла за обедом речь о том, как вычисляется вероятность событий. Молодой математик, оказавшийся среди обедающих, вынул монету и сказал:
— Кидаю на стол монету, не глядя. Какова вероятность, что она упадет гербом вверх?
— Объясните сначала, что значит вероятность, — раздались голоса. — Не всем ясно.
— О, это очень просто! Монета может лечь на стол двояко (рис. 58): вот так — гербом вверх и вот так — гербом вниз.
Всех случаев здесь возможно только два. Из них для интересующего нас события благоприятен лишь один случай. Теперь находим отношение
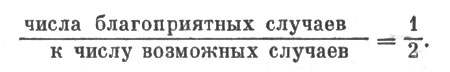
Дробь 1/2 и выражает вероятность того, что монета упадет гербом вверх.
— С монетой-то просто, — вмешался кто-то. — А вы рассмотрите случай посложней, с игральной костью, например.

Рис. 58. ‘Монета может лечь на стол двояко’
— Давайте, рассмотрим, — согласился математик. — У нас игральная кость, кубик с цифрами на гранях (рис. 59). Какова вероятность, что брошенный кубик упадет определенной цифрой вверх, скажем — вскроется шестеркой? Сколько здесь всех возможных случаев? Кубик может лечь на любую из своих шести граней; значит, возможно всего 6 случаев. Из них благоприятен нам только один: когда вверху шестерка. Итак, вероятность получится от деления 1 на 6. Короче сказать, она выражается дробью 1/6.
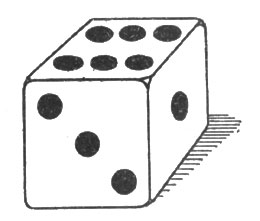
Рис. 59. Игральная кость
— Неужели можно вычислить вероятность во всех случаях? — спросила одна из отдыхающих. — Возьмите такой пример. Я загадала, что первый прохожий, которого мы увидим из окна столовой, будет мужчина. Какова вероятность, что я отгадала?
— Вероятность, очевидно, равна половине, если только мы условимся и годовалого мальчика считать за мужчину. Число мужчин на свете равно числу женщин.
— А какова вероятность, что первые двое прохожих окажутся оба мужчины? — спросил один из отдыхающих.
— Этот расчет немногим сложнее. Перечислим, какие здесь вообще возможны случаи. Во-первых, возможно, что оба прохожих будут мужчины. Во-вторых, что сначала покажется мужчина, за ним женщина. В-третьих, наоборот: что раньше появится женщина, потом мужчина. И, наконец, четвертый случай: оба прохожих — женщины. Итак, число всех возможных случаев — 4. Из них благоприятен, очевидно, только один случай — первый.
Получаем для вероятности дробь 1/4. Вот ваша задача и решена.
— Понятно. Но можно поставить вопрос и о трех мужчинах: какова вероятность, что первые трое прохожих все окажутся мужчины?
— Что же, вычислим и это. Начнем опять с подсчета возможных случаев. Для двоих прохожих число всех случаев равно, мы уже знаем, четырем. С присоединением третьего прохожего число возможных случаев увеличивается вдвое, потому что к каждой из 4 перечисленных группировок двух прохожих может присоединиться либо мужчина, либо женщина. Итого, всех случаев возможно здесь 4 Х 2 = 8. А искомая вероятность, очевидно, равна 1/8, потому что благоприятен событию только 1 случай. Здесь легко подметить правило подсчета: в случае двух прохожих мы имели вероятность 1/2 Х 1/2 = 1/4; в случае трех 1/2 Х 1/2 Х 1/2 = 1/8 случае четырех вероятность равна произведению четырех половинок и т. д. Вероятность все уменьшается, как видите.
— Чему же она равна, например, для десятка прохожих?
— То есть какова вероятность, что первые десять прохожих все подряд окажутся мужчинами? Вычислим, как велико произведение десяти половинок. Это 1/1024, менее одной тысячной доли. Значит, если вы бьетесь о заклад, что это случится, и ставите 1 рубль, то я могу ставить 1000 рублей за то, что этого не произойдет.
— Выгодное пари! — заявил чей-то голос. — Я бы охотно поставил рубль, чтобы получить возможность выиграть целую тысячу.
— Но имеется тысяча шансов против вашего одного, учтите и это.
— Ничего не значит. Я бы рискнул рублем против тысячи даже и за то, что сотня прохожих окажутся все подряд мужчинами.
— А вы представляете себе, как мала вероятность такого события? — спросил математик.
— Одна миллионная или что-нибудь в этом роде?
— Неизмеримо меньше! Миллионная доля получится уже для 20 прохожих. Для сотни прохожих будем иметь… Дайте-ка, я прикину на бумажке. Биллионная… Триллионная… Квадрильонная… Ого! Единица с тридцатью нулями!
— Только всего?
— Вам мало 30 нулей? В океане нет и тысячной доли такого числа мельчайших капелек.
— Внушительное число, что и говорить! Сколько же вы поставите против моего рубля?
— Ха-ха!… Все! Все, что у меня есть.
— Все — это слишком много. Ставьте на кон ваш велосипед. Ведь не поставите?
— Почему же нет? Пожалуйста! Пусть велосипед, если желаете. Я нисколько не рискую.
— И я не рискую. Не велика сумма рубль. Зато могу выиграть велосипед, а вы почти ничего.
— Да поймите же, что вы наверняка проиграете! Велосипед никогда вам не достанется, а рубль ваш можно сказать уже в моем кармане.
— Что вы делаете! — удерживал математика приятель, — Из-за рубля рискуете велосипедом. Безумие!
— Напротив, — ответил математик, — безумие ставить хотя бы один рубль при таких условиях. Верный ведь проигрыш! Уже лучше прямо выбросить рубль.
— Но один-то шанс все же имеется?
— Одна капля в целом океане. В десяти океанах! Вот ваш шанс. А за меня десять океанов против одной капельки. Мой выигрыш так же верен, как дважды два — четыре.
— Увлекаетесь, молодой человек, — раздался спокойный голос старика, все время молча слушавшего спор. — Увлекаетесь…
— Как? И вы, профессор, рассуждаете по-обывательски?
— Подумали ли вы о том, что не все случаи здесь равновозможны? Расчет вероятности правилен лишь для каких событий? Для равновозможных, не так ли? А в рассматриваемом примере… Впрочем, — сказал старик, прислушиваясь, — сама действительность, кажется, сейчас разъяснит вам вашу ошибку. Слышна военная музыка, не правда ли?
— Причем тут музыка?.. — начал было молодой математик и осекся. На лице его выразился испуг. Он сорвался с места, бросился к окну и высунул голову.
— Так и есть! — донесся его унылый возглас — Проиграно пари! Прощай мой велосипед…
Через минуту всем стало ясно, в чем дело. Мимо окон проходил батальон солдат.
