76.Сделать надо так, как показано на рис. 79. Получаются 6 частей, которые для наглядности перенумерованы.
77. Спички следует расположить, как показано на рис. 80, а; площадь этой фигуры равна учетверенной площади спичечного квадрата. Как в этом удостовериться? Дополним мысленно нашу фигуру до треугольника. Получится прямоугольный треугольник, основание которого равно 3, а высота 4 спичкам*. Площадь его равна половине произведения основания на высоту: 1/2 X 3 Х 4 = 6 квадратам со стороною в одну спичку (рис. 80, б). Но наша фигура имеет, очевидно, площадь, которая меньше площади треугольника на 2 спичечных квадрата и равна, следовательно, 4 таким квадратам.
* (Читатели, знакомые с так называемой Пифагоровой теоремой, поймут, почему мы с уверенностью можем утверждать, что получающийся здесь треугольник — прямоугольный: 32 + 42 = 52. )
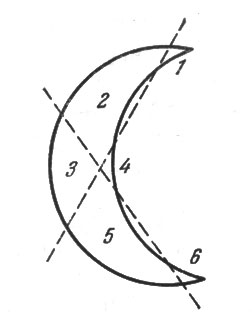
Рис. 79
