Возьмем числа от 1 до 12 и расположим их по кругу (рис. 116). Можно смело взяться угадать задуманное кем-либо число из этого круга.
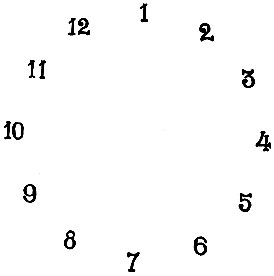
Можно, очевидно, для той же цели взять часы и предложить угадать задуманный кем-либо час.
Можно также пользоваться домино, очками лоте и т. д. Как же угадать задуманное число?
Пусть кто-либо задумает про себя любое из чисел круга. Затем укажите ему сами любое число на этом круге и прибавьте про себя к этому числу 12 (т. е. наивысшее число круга). Вы получите некоторое число, и это число вы скажете громко. Пусть потом задумавший считает про себя от задуманного им числа, притрагиваясь сначала к указанному вами числу, а потом к каждому следующему числу по кругу, идя в обратном порядке, и пусть считает до сказанного вами громко числа. Когда он досчитает до него, последовательно притрагиваясь к числам, то остановится как раз на задуманном им числе или часе.
Пусть, например, кто-либо задумал на круге 5, а вы указываете, например, 9, прибавляете к нему про себя 12 и получите 21. Затем говорите громко задумавшему:
— Считайте про себя, начиная от задуманного вами числа, до 21, но, начиная счет, притроньтесь сначала к 9, потом к 8, потом к 7 и т. д., идя по кругу в обратном порядке, когда же досчитаете до 21, то скажите это число громко и остановитесь.
Задумавший исполнит сказанное ему, и когда досчитает до 21, то как раз сам укажет задуманное им число 5.
Можно обставить эту задачу еще таинственнее, например, так.
Кто-нибудь задумывает какое-нибудь число (например, 5). Вы берете, например, число 9, прибавляете к нему мысленно 12, получаете 21 и говорите задумавшему:
— Теперь я буду стучать карандашом (или пальцем), и при каждом стуке вы прибавляете про себя к задуманному вами числу по единице. Но, когда досчитаете до 21, скажите громко: "21".
Затем стучите по 9, по 8, по 7 и т. д. …, по 12, по 11 и т. д. … Задумавший число в это время про себя будет считать 5, 6, 7 и т. д., но когда скажет громко: "21", то окажется, что вы стучите как раз по задуманному им числу.
— Вы задумали число 5!- говорите вы ему.
— Совершенно верно!- ответит вам задумавший, дивясь, как вы могли узнать это, если он сам не знает, в чем разгадка этого будто бы фокуса.
Решение. "Фокуса" здесь, конечно, нет, а есть только правильный математический расчет.
Чтобы от 5 прийти к 9, нужно считать так: 5, 6, 7, 8, 9. Значит, от 9 до 5 нужно пройти через те же числа 9, 8, 7, 6, 5, только считая их в обратном порядке. Если, указывая на 9, мы скажем "пять", затем, указывая на 8, скажем "шесть" и т. д., то, придя к задуманному числу 5, скажем "девять". Если затем идти по кругу в том же направлении и присчитать к "девяти" еще 12 последовательных чисел круга, то опять приходим к тому же числу 5. Дело сводится, следовательно, к счету по кругу в обратном направлении от указанного числа 9 до 9 + 12, т. е. до 21.
Если, наоборот, задумано 9, а указано 5, то от 9 до 5, считая в прямом направлении по кругу (по порядку возрастания чисел), получаем: 9, 10, 11, 12, 12+1, 12 + 2, 12 + 3, 12 + 4, 12 + 5, т.е. 17. Следовательно, начиная с 5, можно прийти к задуманному числу 9, идя в обратном направлении и отсчитывая те же 5 + 12 = 17 чисел.
