Хозяин устроил в своем погребе шкаф в форме квадрата с девятью отделениями. Среднее (внутри) отделение он оставил свободным для пустых бутылок, а в остальных расположил 60 бутылок вина так, что в каждом угловом отделении их было по 6, а в каждом из средних по 9. Таким образом, на каждой стороне квадрата было по 21 бутылке. Слуга подметил, что хозяин проверяет число бутылок, только считая бутылки по сторонам квадрата и следя за тем, чтобы на каждой стороне квадрата было по 21 бутылке. Тогда слуга унес сначала 4 бутылки, а остальные расставил так, что вновь получилось по 21 на каждой стороне. Хозяин пересчитал бутылки своим обычным способом и подумал, что бутылок остается то же число и что слуга только переставил их. Слуга воспользовался оплошностью хозяина и снова унес 4 бутылки, расставив остальные так, что на каждой стороне квадрата выходило опять по 21 бутылке. Так он повторял, пока было возможно. Спрашивается, сколько раз он брал бутылки и сколько всего бутылок он унес?
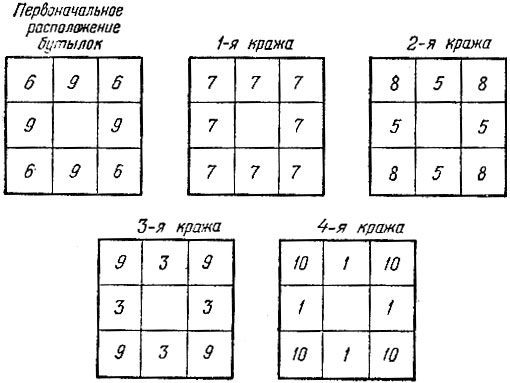
Рис. 58
Решение. Слуга брал себе по бутылке из каждого среднего отделения и из тех же отделений, чтобы обмануть хозяина, после каждого воровства прибавлял по бутылке в угловые отделения. Так он воровал 4 раза по 4 бутылки, а всего, значит, унес 16 бутылок. Все это видно из рис. 58. Слуга мог расставлять бутылки и другими способами. Но всегда в первом и третьем столбцах квадрата он должен был бы оставлять по 21 бутылке и потому не мог бы унести более 60-2-21 = 18 бутылок, т. е. совершить более четырех краж.
