Определение электроемкости. Физическая величина, характеризующая способность двух проводников накапливать электрический заряд, называется электроемкостью.
Конденсаторы. Устройство, состоящее из двух изолированных друг от друга проводников, расположенных на близком расстоянии друг от друга, называется конденсатором . Независимо от формы проводников их называют пластинами конденсатора. Простейший конденсатор состоит из двух плоскопараллельных пластин, размеры которых много больше расстояния между пластинами (l >> d) . Если подключить пластины к источнику напряжения (батарее), то между пластинами возникнет разность потенциалов U , а сами пластины после установления равновесия окажутся противоположно заряженными зарядами +q -q , которые перетекли на пластины из батареи. Когда говорят, что конденсатор заряжен, подразумевают наличие ненулевого заряда на одной из пластин . В целом же конденсатор электрически нейтрален.
Опыт показывает, что увеличение разности потенциалов между пластинами приводит к пропорциональному увеличению заряда на пластинах, так что отношение
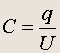 (6.1)
(6.1)
остается постоянным.
Электроемкостью двух проводников называется отношение заряда одного из проводников к разности потенциалов между проводниками . Единицей электроемкости является фарада (Ф):
[C] = Ф = Кл/В .
Вычисление электроемкости плоского конденсатора. Поле, создаваемое бесконечной заряженной проводящей пластиной с плотностью заряда s равно Е = s /(2 e 0 ).
Если приблизить друг к другу две проводящие пластины, размеры которых много больше расстояния между ними, и подключить их к источнику напряжения, то можно считать, что поле, создаваемое каждой из пластин, приближенно совпадает с полем бесконечной пластины. Тогда внутри получившегося плоского конденсатора (между пластинами) поле будет равно сумме полей, создаваемых каждой пластиной:
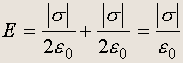
Так как | s | = q/S , где S — площадь пластины, то напряженность поля между пластинами равна
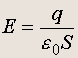
Таким образом, если пренебречь краевыми эффектами, поле между пластинами плоского конденсатора однородно. Точность этого утверждения тем выше, чем больше размер пластин по сравнению с расстоянием между ними.
Пользуясь формулой U = Ed , получаем:
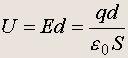
откуда
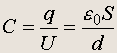 (6.2)
(6.2)
Последовательное соединение конденсаторов.
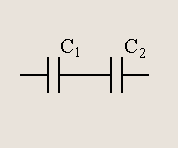
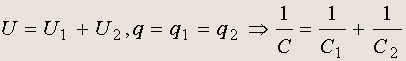 (6.3)
(6.3)
Параллельное соединение конденсаторов.
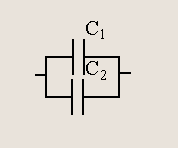
![]() (6.4)
(6.4)
Энергия заряженного конденсатора. Работа, совершаемая батареей при заряжании конденсатора, переходит в потенциальную энергию заряженного конденсатора. В процессе зарядки в каждый момент времени разность потенциалов между пластинами равна U’ = q’/C , где q’ — мгновенное значение заряда на пластине . При переносе на пластину заряда dq’ потенциальная энергия конденсатора увеличивается на величину dW п = U’ dq’ .
Поэтому
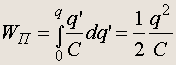 (6.5)
(6.5)
Формулу для энергии заряженного конденсатора можно записать в нескольких эквивалентных формах:
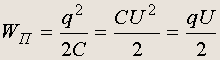
Энергия электростатического поля. Формулу для энергии, запасенной в плоском конденсаторе, можно записать в следующем виде:
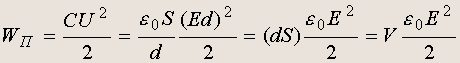
Здесь V — объем области между пластинами конденсатора. Поэтому можно определить понятие плотности энергии в пространстве между пластинами, равной энергии, приходящейся на единицу объема:
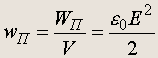 (6.6)
(6.6)
Из этой формулы следует, что энергия взаимодействия заряженных пластин конденсатора может быть выражена через напряженность электрического поля между пластинами. Этим подтверждается материальный характер электрического поля.
