§ 5. Геометрические построения → номер 14
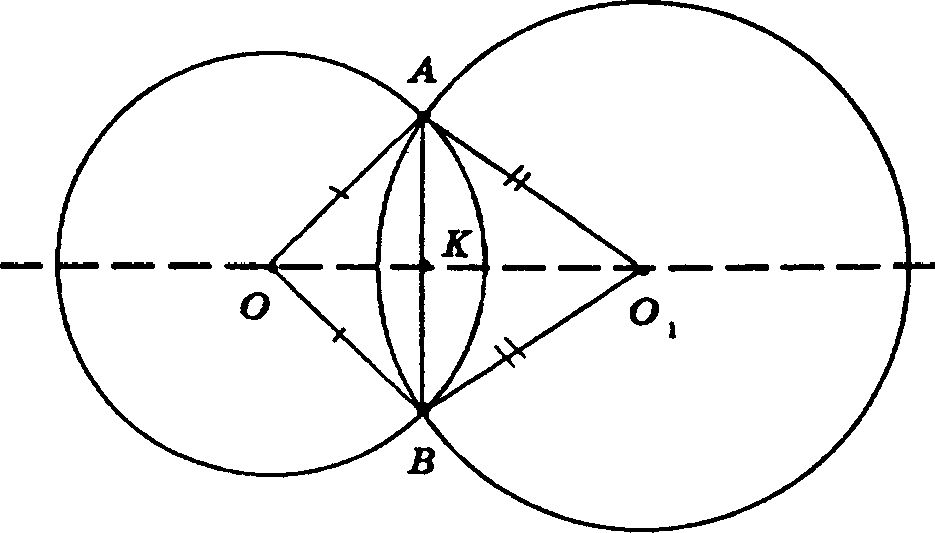
1) Докажем, что АВ ⊥ ОО1.
В ΔОАО1 и ΔОВО1:
ОА = ОВ (как радиусы),
О1А = О1В (как радиусы),
ОО1 — общая.
Таким образом, ΔОАО1 = ΔОВО1 по 3-му признаку равенства треугольников, откуда ∠AOK = ∠KOB, ∠AO1K = ∠BO1K.
В ΔАОВ:
ОА = ОВ, следовательно, ΔАОВ — равнобедренный, ∠AOK = ∠KOB, таким образом, OK — биссектриса, которая является и высотой, т. к. ΔАОВ — равнобедренный, то есть OK ⊥ АВ.
Таким образом, АВ ⊥ ОО1.
2) Докажем, что окружности не могут пересекаться более чем в двух различных точках.
Допустим, что две окружности с центрами О и О1 пересекаются хотя бы в трех различных точках А, В, С, тогда из п. 1 АС ⊥ ОО1, АВ ⊥ ОО1, но это невозможно, так как через данную точку А можно провести одну и только одну прямую, перпендикулярную ОО1.
Таким образом, мы пришли к противоречию.
