§ 5. Геометрические построения → номер 16
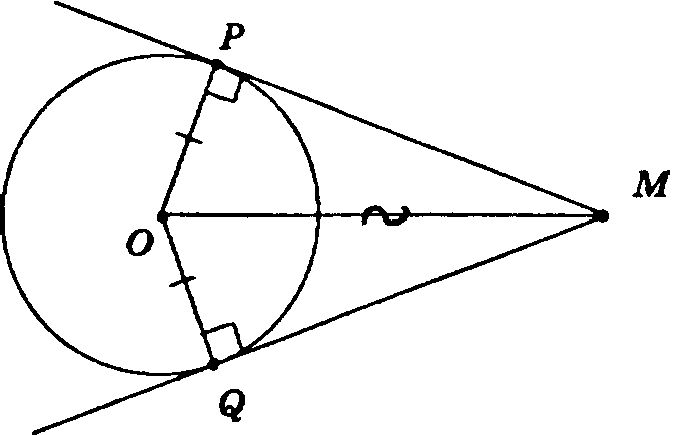
1) В ΔОРМ и ΔOQM:
ОМ — общая,
ОР = OQ, как радиусы,
ОР ⊥ МР, OQ ⊥ MQ (т. к. МР и MQ — касательные).
Таким образом, ΔОРМ = ΔOQM по 1-му признаку равенства треугольников. Откуда МР = МQ.
2) Пусть через точку М можно провести три касательных к окружности: МР, MQ, МА. Тогда из п. 1 следует, что МР = MQ = MA, откуда точки Р, Q, А лежат на одной окружности с центром М. Получилось, что две окружности имеют три общие очки. Противоречие. В задаче 14 § 5 мы это доказали. Таким образом, через данную точку нельзя провести более двух касательных к данной окружности.
