№ 2. Через середину О отрезка АВ проведена прямая, перпендикулярная прямой АВ. Докажите, что каждая точка Х этой прямой одинаково удалена от точек А и В

§ 3. Признаки равенства треугольников → номер 2

Возьмем на прямой произвольную точку Х и соединим ее с точками А и В.

Рассмотрим полученные треугольники: В ΔАОХ = ΔВОХ АО = ОВ, т. к. О — середина отрезка АВ;

∠AОХ = ∠BОХ = 90°, т. к. АВ⊥ХО;

ОХ — общая сторона.

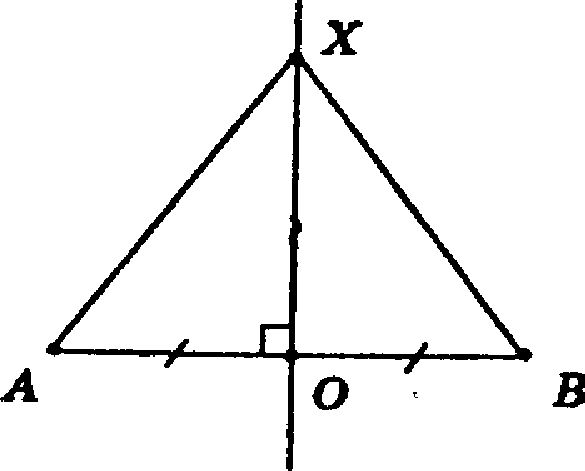
Таким образом, ΔАОХ = ΔВОХ по 1-му признаку равенства треугольников. В равных треугольниках против равных углов лежат равные стороны. Отсюда АХ=ВХ.

Что и требовалось доказать.