§ 3. Признаки равенства треугольников → номер 20
1) ∠BAK = ∠KAC = ∠OCA = ∠OCK, т. к. ∠A = ∠C, и СО и КА — биссектриссы.
В ΔAKB и ΔСОВ: АВ = ВС (т. к. ΔАВС — равнобедренный) ∠BAK = ∠BCO (т. к. АК и СО — биссектриссы равных углов). ∠B — общий. Таким образом, ΔAKB = ΔСОВ по 2-му признаку равенства треугольников.
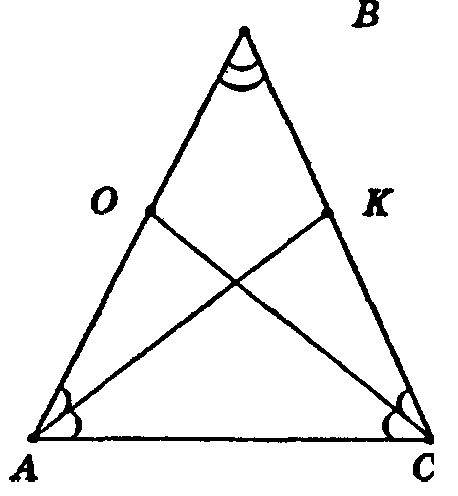
Откуда AK = СО, что и требовалось доказать.
2) AQ = QB = BF = FC, т. к. AF и CQ — медианы. В ΔAFB и ΔCQB:
АВ = ВС (т. к. ΔАВС — равнобедренный)
QB = BF
∠В — общий. Таким образом, ΔAFB = ΔCQB по 1-му признаку равенства треугольников.
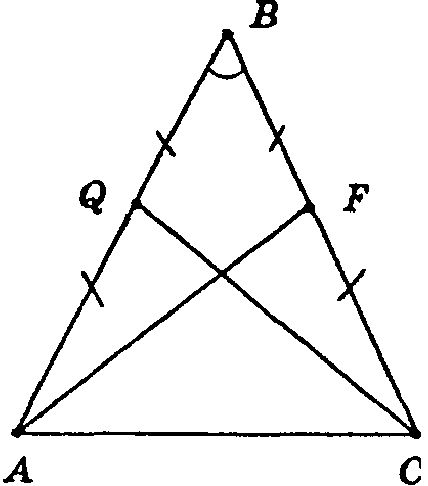
Откуда AF = CQ.
