§ 5. Геометрические построения → номер 4
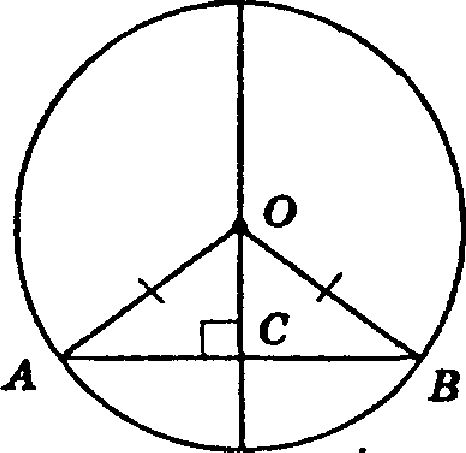
Теорема: Доказать, что диаметр окружности, препендикуляр-ный хорде, проходит через ее середину.
В ΔАОС и ΔСОВ:
ОА = ОВ, т. к. ОА и ОВ — радиусы окружности, СО — общая сторона, таким образом, ΔАОС = ΔОСВ по гипотенузе и катету, откуда АС = СВ.