Дано:
Дана правильная треугольная пирамида TABC, в основании которой лежит треугольник (АВС) со стороной 10 см. Найти площадь сечения пирамиды плоскостью, проходящей через точку N ребра AT так, что AN = 3*NT, через точку K ребра AB так, что AK = KB, если сечение параллельно медиане AD треугольника АВС и находится на расстоянии от неё (от медианы), равном 5*(3^0.5)/4 см.
Решение
Сделаем дополнительные построения (рис.1)

Во-первых, построим сечение пирамиды плоскостью, проходящей через точки N и K паралелельно AD (назовем её π).
При этом будем применять нотацию (способ записи), как в задаче Сечение пирамиды плоскостью, параллельной медиане её боковой грани (№1)
Пусть p(KE,AD), тогда in(KE,π) и in(KE,ABC) (т.к in(K,AB)) => t(KE,BC). Пусть t(KE,BC)=E.
Т.к. in(KN,TAB), то t(KN,TB). Пусть t(KN,TB)=F =>
Т.к. in(KN,π), то in(F,π) (1)
{(1),in(E,π)} => in(FE,π)
Но кроме этого in(FE,TBC) => t(FE,TC). Пусть t(FE,TC)=G => KNGE – сечение пирамиды пл-тью π.
Построим теперь отрезок, длина которого равна d(AD,π).
Т.к. AI – медиана ABC и ABC – равносторонний, то n(AI,BC).
Пусть p(AI,BC), тогда in(AI,ABC) и n(AI,AD).
Пусть n(TO,ABC), тогда in(O,AD) и l(OD)=1/3*l(AD)
Пусть p(AH,TO), тогда n(AH,ABC) и n(AH,AD) => n(AD,AHI) и A=op(AD,AHI) (3).
Остается построить op(π,AHI)
Т.к. p(KE,AD), то in(KE,ABC) => t(KE,AI). Пусть t(KE,AI)=I => I=op(KE,AHI) (2).
Пусть p(NH,AD), тогда in(NH,TAO).
Т.к. p(AH,TO), то in(AH,TAO) => t(NH,AH). Пусть
t(NH,AH)=H => H=op(N,AHI). Учитывая также (2),
Рис.1.Сечение KNGE и расстояние AJ
получаем: HI=op(π,AHI).
Пусть in(AJ,AHI) и n(AJ,HI), тогда, учитывая (3): l(AJ)= d(AD,π).
Целевой отрезок построен.
Приступим к мат.модели задачи. Далее величины выделены так: искомые и определяемые.
Из n(HAI) по т-ме Пифагора HI=fg(HA,AI) (как гипотенуза) (1)
Кроме того, s(HAI)=1/2*HA*AI и s(HAI)=1/2*AJ*HI => HI= HA*AI/AJ (2)
Учитывая, что AJ=5/4*√3 и (1), получим q1(HA,AI) => HA=f1(AI).
Ввиду p(AD,IE) AI=DE. А ввиду AK=1/2*AB DE=1/2*DB (по т-ме Фалеса). DB=1/2*BC=1/2*10 (по условию з-чи).
Пусть p(GG1,EK), тогда in(GG1,π) => t(GG1,HI). Пусть t(GG1,HI)=G2.
Пусть p(KN2,HI), тогда in(KN2,π) => t(KN2,GG1) и t(KN2,HN). Пусть t(KN2,GG1)=G1, t(KN2,HN)=N2.
Очевидно также, что t(KN,GE). Пусть t(KN,GE)=N1.
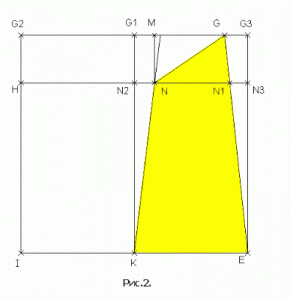
Изобразим сечение KNGE (со вспомогательными построениями в этой плоскости) на отдельном чертеже (рис.2).
Отсюда видно, что:
s(KNGE)=s(KG1G3E)-s(KN2N)-s(N2G1MN)-s(NMG)-s(GG3E) (3)
Чтобы найти все эти площади: N2N=? NM=? GG3=?
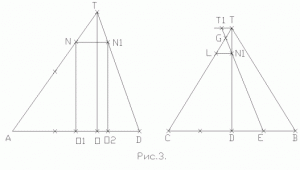
Ответы на эти вопросы ясны из рис.3.
Т.к. p(NN1,AD), то TN1=1/3*N1D (по т-ме Фалеса), а из g(N1O2D,TOD) => N1D=3/4*TD
Пусть p(NO1,TO) и p(N1O2,TO), тогда соответственно O1O=1/4*AO и OO2=1/4*OD => O1O2=1/4*AD=NN1
Т.к. NO1=HI, то из g(NO1A,TOA) и TN=1/3*AN (по у.з.) => TO=HI*TA/AN=4/3*HI
Из n(TOD) TD=fg(TO,OD) (по т-ме Пифагора)
OD=1/3*AD (т.к. пирамида – правильная).
AD найдется как высота равностороннего ABC.
Теперь обратимся к рис.3б.
Здесь p(N1L,BC), p(TT1,BC).
Из n(N1DE) найдется N1E=fg(N1D,DE) (DE=1/2*DB=1/4*BC=10/4=5/2)
GN1=?
Из g(T1TN1,EDN1) T1T=DE*TN1/N1D=1/3*DE
Из g(TN1L,TDC) LN1=1/4*CD, CD=1/2*BC
Из g(LGN1,CGE) GN1=GE*LN1/CE
CE=3/4*BC => GN1=GE*1/6
N1E=GE-GN1=GE*(1-LN1/CE)=GE*5/6 => GE=N1E/(5/6)
Возвращаемся к рис.2
Из g(N1N3E,GG3E)
N1N3=GG3*N1E/GE= GG3*5/6
G3E=N3E*GE/N1E=N3E/(5/6), N3E=HI
Из n(GG3E) по т-ме Пифагора GG3=fс(GE,G3E) (как катет)
G3N3=G3E-N3E=NM
N2N=N2N3-NN1-N1N3
N2N3=KE=1/2*AD
Подставляя найденные значения в (3), получим искомую площадь.