Консервативные системы. В природе существуют такие взаимодействия, что порождаемые ими силы обладают замечательным свойством: работа этих сил при перемещении тела по замкнутому пути равна нулю. Такие силы называют консервативными , а системы, в которых действуют только консервативные силы, называют консервативными системами .
Примером консервативных сил может служить гравитационная сила. При движении тела в однородном гравитационном поле совершаемая работа равна
![]()
Если тело, падающее с высоты h 1 до высоты h 2 , затем опять поднимается на высоту h 1 , совершаемая при этом работа равна нулю.
Другим примером консервативной силы может служить электростатическая сила притяжения или отталкивания электрических зарядов или упругая сила сжатой пружины.
Пример неконсервативных сил: сила трения.
Потенциальная энергия. Как следует из приведенных выше формул, при движении под действием консервативных сил совершаемая работа определяется разностью значений определенной величины, зависящей только от положения тела в пространстве. Назовем потенциальной энергией тела в однородном поле сил тяжести величину
![]() (15.1)
(15.1)
Тогда работа по перемещению тела из одной точки к другой будет равна:
![]()
Потенциальная энергия сжатой пружины:
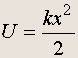 (15.2)
(15.2)
Во всех случаях по определению изменение потенциальной энергии, т. е. разность между конечным и начальным значением потенциальной энергии, равна взятой со знаком минус работе консервативных сил: D U = — A .
Потенциальная энергия может быть всегда изменена добавлением произвольной постоянной, так как физический смысл имеет только разность значений потенциальной энергии в двух точках. Это позволяет выбирать произвольным образом начало отсчета потенциальной энергии.
Закон сохранения механической энергии. Работа, совершаемая консервативными силами, действующими на тело, равна, с одной стороны, изменению кинетической энергии тела, а с другой — взятому со знаком минус изменению потенциальной энергии. Поэтому
![]()
или
![]() (15.3)
(15.3)
Таким образом, для отдельно взятого тела сумма кинетической и потенциальной энергии этого тела сохраняется в процессе движения.
Для консервативной системы справедлив закон сохранения механической энергии.
В консервативной системе полная механическая энергия сохраняется.
Это означает, что при эволюции системы во времени энергия может переходить из одной формы в другую (кинетическая энергия — в потенциальную, и наоборот), но сумма этих двух величин не зависит от времени.
