Уравнение малых колебаний. Если тело, прикрепленное к упругой пружине, вывести из состояния равновесия, то на тело начнет действовать упругая сила со стороны пружины, которая по закону Гука пропорциональна отклонению тела от положения равновесия. Следует помнить, что закон Гука справедлив только для малых отклонений от положения равновесия (количественно это выражается неравенством D x << l , где l - длина нерастянутой пружины). поэтому колебания, происходящие под действием сил, линейно зависящих от отклонения тела от положения равновесия, называют малыми колебаниями . система, совершающая малые колебания, называется гармоническим осциллятором .
Уравнение движения гармонического осциллятора имеет вид:
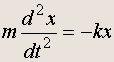(20.1)
Его можно переписать в другой форме, введя обозначение w 2 = k/m . Тогда
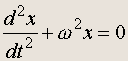(20.2)
Это есть математическое уравнение малых колебаний .
Гармонические колебания. Уравнение Ньютона, приведенное выше, имеет решение в виде гармонического колебания.
Простое одномерное гармоническое колебание — такое движение, при котором координата тела зависит от времени по закону
(20.3)
Величина A называется амплитудой колебаний (максимальное отклонение от положения равновесия), w — циклическая, или круговая, частота колебаний ([ w ] = Гц = с -1 ) , j 0 — начальная фаза колебаний.
Главной особенностью выписанного решения является то, что каждое значение x в силу периодичности косинуса повторяется через один и тот же промежуток времени, называемый периодом T ([T] = c) . Действительно, если аргумент косинуса изменится на угол 2p радиан, то значение косинуса не изменится. Назовем периодом тот интервал времени, за который аргумент косинуса меняется на 2p . Тогда
откуда
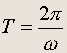(20.4)
По определению частота
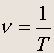(20.5)
([ n ] = Гц = с -1 ) .
Подставляя выражение для Т через круговую частоту w , находим соотношение:
(20.6)
Следует отметить, что можно с тем же результатом описывать гармоническое колебание функцией sin( w t + j 0 ) , что эквивалентно иному выбору начальной фазы.
Последовательно дифференцируя выписанное решение по времени, можно получить выражения для скорости и ускорения колеблющегося тела в любой момент времени.
Скорость:
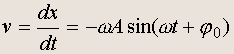(20.7)
Ускорение:
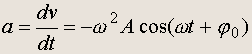(20.8)
Энергия гармонического осциллятора. Полная энергия гармонического осциллятора:
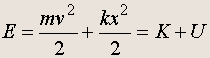
Если подставить приведенные выше выражения для x и v в формулу для полной энергии, получим
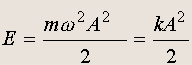(20.9)
Полная энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний и не зависит от времени.
Математический маятник . На невесомой нити длиной l подвешен груз массой m , совершающий колебания относительно положения равновесия. Нулевое значение потенциальной энергии выбрано в точке равновесия, тогда в произвольном положении
где угол отклонения маятника от положения равновесия q однозначно
определяет положение груза в любой момент времени.
Это уравнение точное, однако его решение сложно. Представим теперь, что маятник совершает малые колебания. В этом случае q << 1 и можно сделать замену: sin q " q . уравнение малых колебаний математического маятника приобретает вид уравнения для гармонического осциллятора:
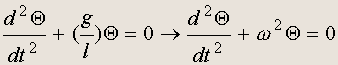(20.10)
где введено обозначение w = (g/l) 1/2 . Этой формулой определяется частота колебаний математического маятника. Период колебаний математического маятника равен
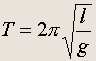(20.11)