Внутренняя энергия. В рамках молекулярно-кинетической теории внутренняя энергия макроскопического тела U определяется как среднее значение суммы всех кинетических энергий хаотического движения молекул или атомов тела и потенциальных энергий взаимодействия всех молекул друг с другом. Вычисление внутренней энергии произвольного тела представляет очень сложную (иногда невыполнимую) задачу. Для идеального газа задача упрощается, так как в этом случае потенциальной энергией взаимодействия молекул (атомов) пренебрегают. Таким образом, внутренняя энергия идеального газа равна среднему значению суммарной кинетической энергии молекул газа, заполняющих данный объем: U = N , где — средняя кинетическая энергия молекул. Так как = (3/2)kT , то приходим к формуле:
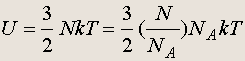
выражающей внутреннюю энергию идеального газа через его температуру Т и количество молей газа. Иначе формулу можно представить в виде:
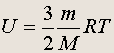 (5.1)
(5.1)
Эта формула справедлива для идеального одноатомного газа, атомы которого движутся только поступательно. Из нее следует, что внутренняя энергия идеального газа есть функция только температуры газа и его количества и не зависит от занимаемого газом объема.
Для реальных газов, жидкостей и твердых тел внутренняя энергия является функцией как температуры, так и объема.
Закон равнораспределения. У атомов идеального одноатомного газа имеются три степени свободы (каждый атом может двигаться поступательно вдоль одной из трех осей декартовой системы координат). Однако у более сложных многоатомных газов молекулы состоят из двух или нескольких атомов, связанных вместе за счет сил взаимодействия. Наглядно можно представить себе простейшие модели молекул двухатомных газов в виде жестких гантелей или гантелей с пружинками, позволяющих атомам вращаться и колебаться относительно друг друга. У таких систем количество степеней свободы больше трех (добавляются еще вращательные и колебательные степени свободы). Формулу для средней кинетической энергии поступательного движения атомов одноатомного газа можно записать в виде = 3(kT/2) и понимать ее так, что на каждую степень свободы приходится в среднем энергия kT/2 . Общее утверждение, доказываемое в статистической механике (раздел физики, обосновывающий основные положения термодинамики в рамках молекулярно-кинетической теории), можно сформулировать в виде теоремы о равнораспределении .
Для системы N молекул, имеющих s степеней свободы каждая, и находящейся в тепловом равновесии при температуре , средняя механическая энергия равна s(kT/2) .
(Следует заметить, что при формулировке теоремы учитываются только поступательные и вращательные степени свободы, а колебательные степени свободы при обычных температурах «заморожены», так как их характерные температуры гораздо выше комнатных.)
Работа в термодинамике. Энергия, передаваемая системе или от системы к окружающей среде только за счет разности температур, называется количеством теплоты. Всякая иная энергия, которая передается от системы к окружающим телам или от них к системе независимо от разности температур между ними, называется работой . Если сама система совершает работу (т. е. энергия передается от системы к внешним телам), то принято считать работу положительной: А > 0 . Если внешние тела совершают работу над системой (энергия поступает внутрь системы), то работа считается отрицательной: А < 0 .
Работа, совершаемая при изменении объема газа
![]()
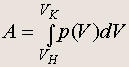 (5.2)
(5.2)
Работа при изобарическом процессе
![]()
но р = const , поэтому
![]() (5.3)
(5.3)
Работа при изотермическом процессе
В этом случае р(V) = n RT/V , поэтому
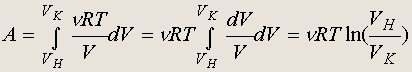 (5.4)
(5.4)
Работа при адиабатическом процессе (без вывода)
Уравнение адиабаты для идеального газа (адиабата — процесс изменения состояния, идущий без теплообмена с окружающей средой): pV g = const , где g = c p /c V — отношение теплоемкостей при постоянном давлении и постоянном объеме.
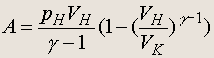 (5.5)
(5.5)
